
第三章 多维随机变量及其分布 3.1 二维随机变量


 二维离散型随机变量的分布律可以这样表示:
二维离散型随机变量的分布律可以这样表示: 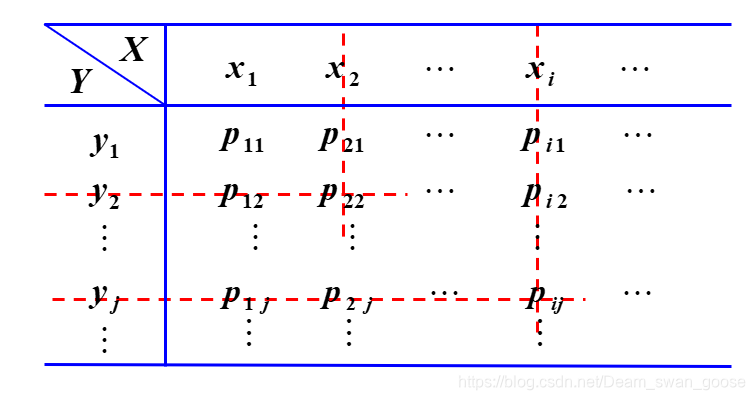 例1:
例1: 
 离散型的比较简单,分布律就从原来的一维表格变成二维的表格。
离散型的比较简单,分布律就从原来的一维表格变成二维的表格。 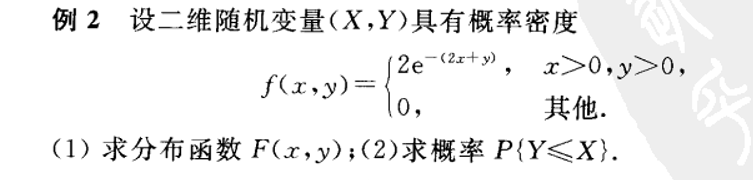
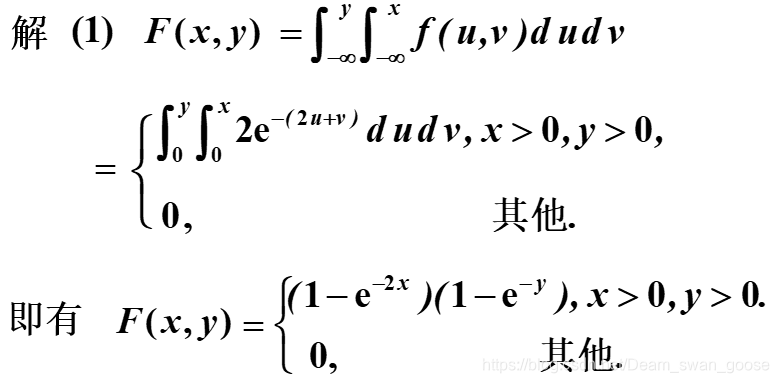
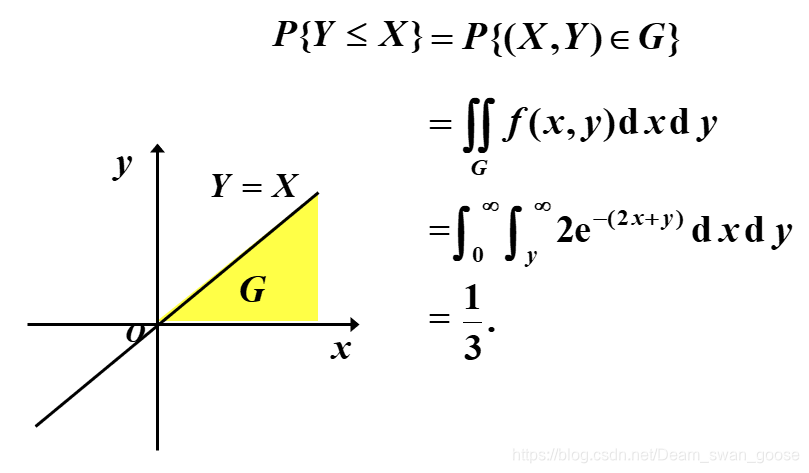 小结:
小结: 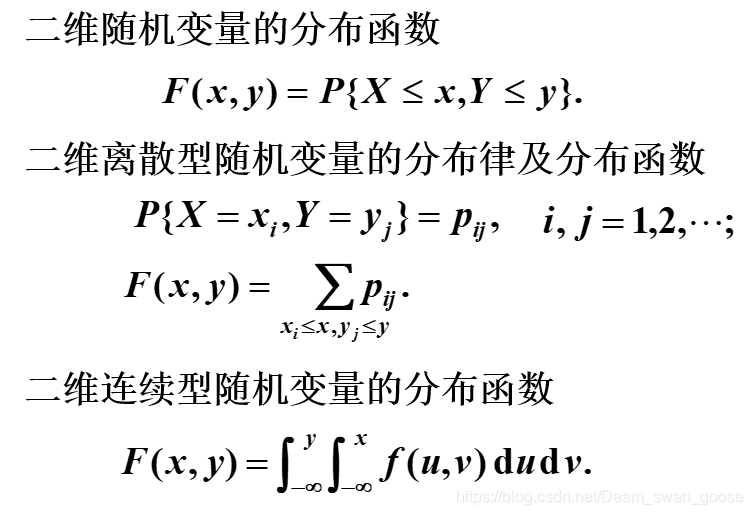
发布日期:2021-05-06 10:56:17
浏览次数:23
分类:技术文章
本文共 526 字,大约阅读时间需要 1 分钟。
3.1 二维随机变量
文章目录
二维随机变量及其分布函数
上一章里我们都是用一个随机变量 X X X来表述概率的。但是在现实生活里影响事情发生概率的随机变量通常不止一个,所以我们在这一章中引入多维随机变量。这里先从最简单的二维随机变量开始。

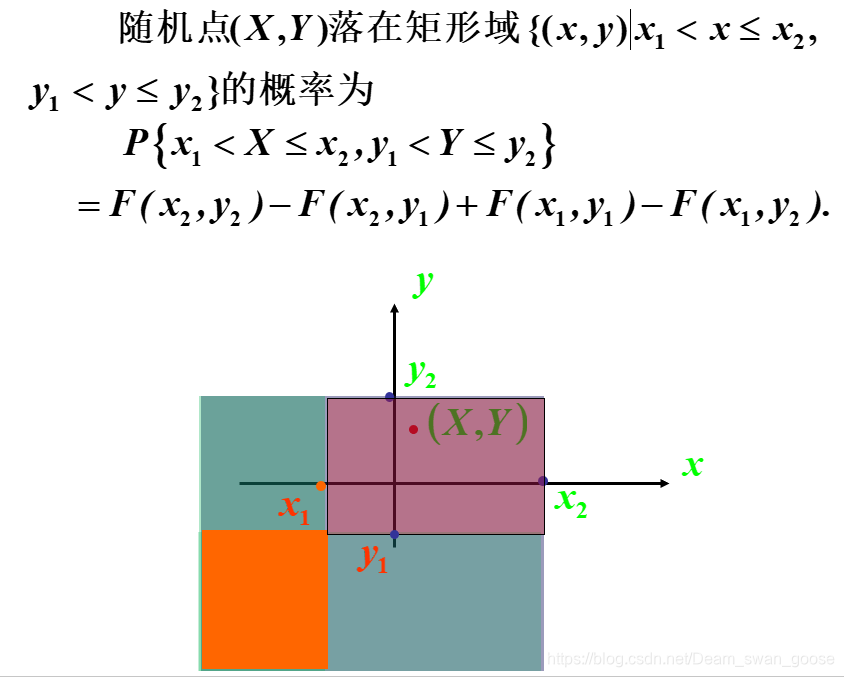
性质:


二维离散型随机变量
定义:
 二维离散型随机变量的分布律可以这样表示:
二维离散型随机变量的分布律可以这样表示:  例1:
例1: 
 离散型的比较简单,分布律就从原来的一维表格变成二维的表格。
离散型的比较简单,分布律就从原来的一维表格变成二维的表格。 二维连续型随机变量


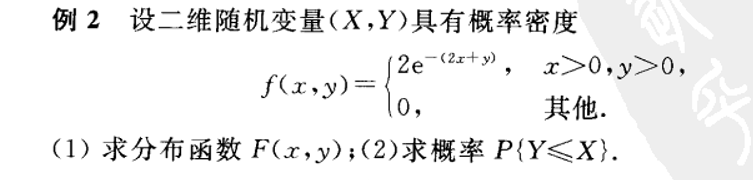
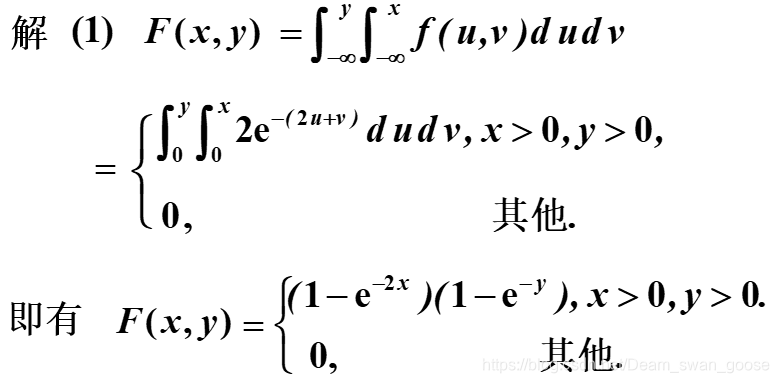
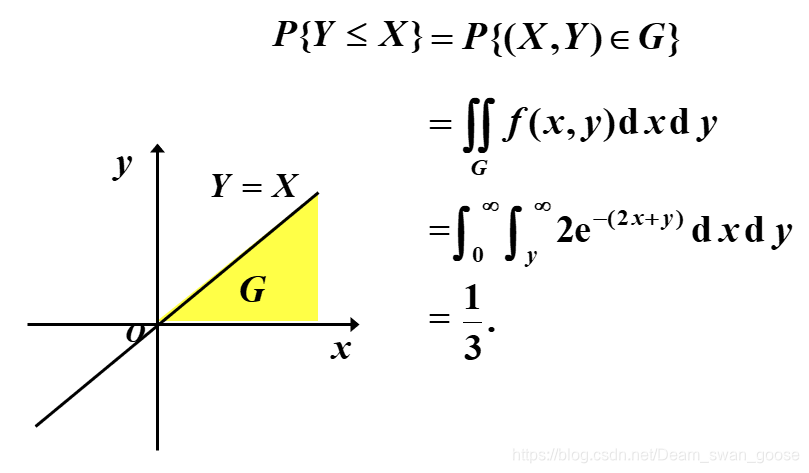 小结:
小结: 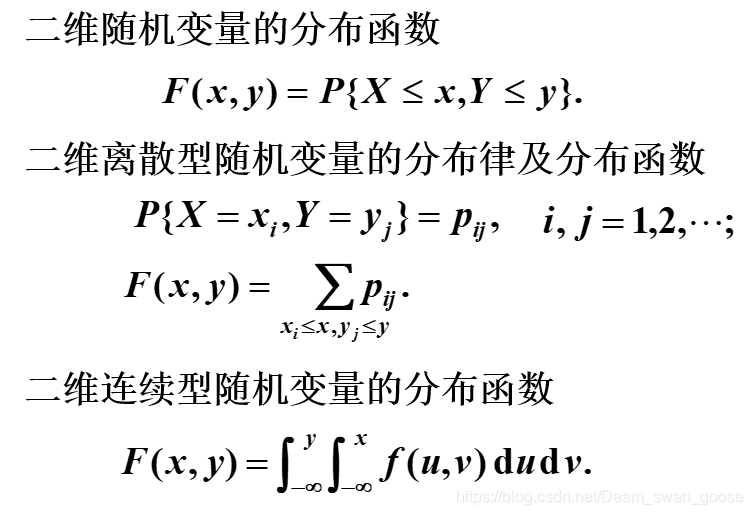
发表评论
最新留言
第一次来,支持一个
[***.219.124.196]2025年03月14日 01时41分56秒
关于作者

喝酒易醉,品茶养心,人生如梦,品茶悟道,何以解忧?唯有杜康!
-- 愿君每日到此一游!
推荐文章
poj3617
2019-03-04
poj3069
2019-03-04
Java洛谷P5461 赦免战俘讲解
2019-03-04
关于 form表单 嵌套问题的解决方案
2019-03-04
论转发与重定向参数传递问题(jsp+servlet项目开发遇到的问题)
2019-03-04
Android—— log.e(),log.d(),log.i()等的区别
2019-03-04
js中时间戳转时间格式
2019-03-04
位运算
2019-03-04
MarkDown
2019-03-04
nginx 配置实例 - 反向代理(1)
2019-03-04
c++ 函数化 面向对象
2019-03-04
【无需额外安装插件】vscode 同步插件、设置、UI状态 | 超简单方法
2019-03-04
【unity shader 入门精要】CH2 渲染流水线
2019-03-04
【unity shader 入门精要】CH7 基础纹理
2019-03-04
java学习笔记6:windows、linux安装配置jdk
2019-03-04
java学习笔记24:文档注释与代码块
2019-03-04
java学习笔记31:Arrays类介绍使用
2019-03-04
java学习笔记36:Integer的基本方法
2019-03-04