本文共 1777 字，大约阅读时间需要 5 分钟。

数据的表示

n进制转十进制

• 例如二进制转十进制：10100.01 = 1x2^4 +1x2^2 + 1x2^-2
• 例如七进制转十进制：604.01 = 6x7^2 + 4x7^0 + 1x7^-2

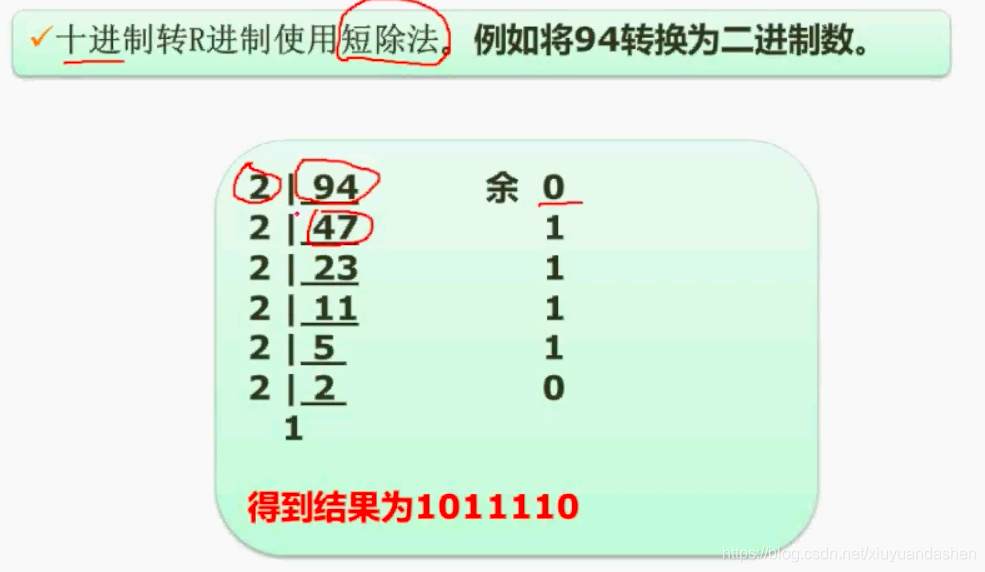
十进制转n进制 使用短除法

• 例如将94转为二进制
  • 

二进制转八进制和十六进制

• 二进制转八进制只需要对二进制数从右边开始每三个一组转成八进制，最高位如果不足三位数就在最左边补0。
• 二进制转十六进制只需要对二进制数从右边开始每四个一组转成16进制，最高位如果不足四位就在最左边补0。
• 我们可以对十六进制转成二进制，只需要将每个位拆成4位二进制数就得到对应对二进制，然后对转成的二进制从右边到左边三位划分就转成八进制了。

原码、反码、补码以及移码

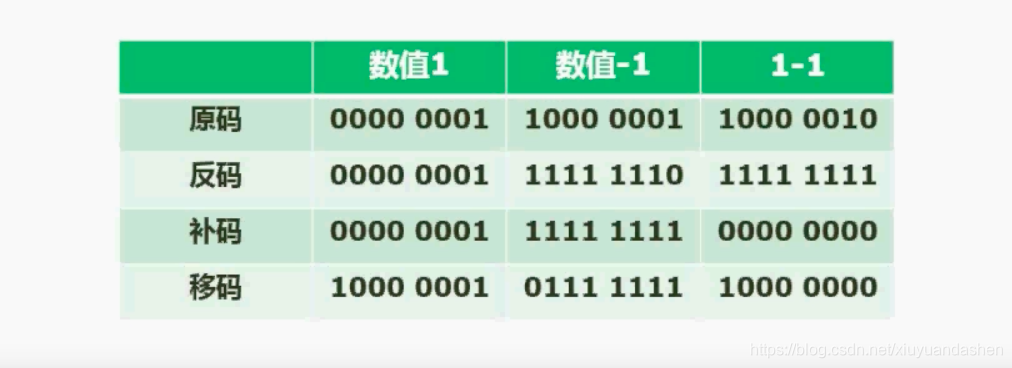
从上图中可以看出 ，原码是不适合做计算的！因为原码是1-1居然等于10000010。

• 原码总共八位，首位为符号位。正数的符号位为0，负数的符号位为1。
• 反码：正数的反码就是其本身，负数的反码是符号位不变，其他位取反。
• 补码：正数的补码就数其本身，负数的补码是其反码的基础上加1。
• 移码：在补码的基础上将符号位取反。

数值表示范围 由于负数的补码在其反码的基础上加1，所以范围会比其他数多1。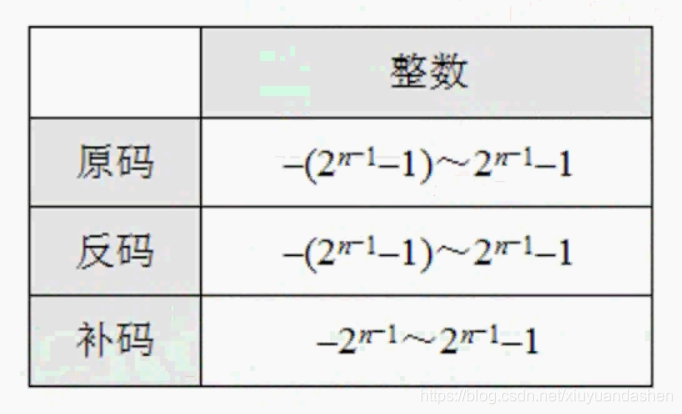

浮点数运算

浮点数运算首先要将指数统一，然后尾数进行相互计算，最后格式化结果(小数点前不超过1位数)。

• 例如 ： 1.0x 10^3 + 1.19x10^2 = 1.0 x10^3 + 0.119x10^3 = 1.119x10^3;

  计算机结构

  

计算机体系结构分类 - Flynn

CISC 和 RISC

流水线

流水线是指在程序执行时多条指令重叠进行操作的一种准并行 处理实现技术。各种部件同时处理是针对不同指令而言的，它们可同时为多条指令的不同部分进行工作，以提高各部件的利用率和指令的平均执行速度。

流水线计算

流水线时间计算

流水线吞吐率计算

表示一个流水线的周期

流水线的加速比计算

流水线的效率

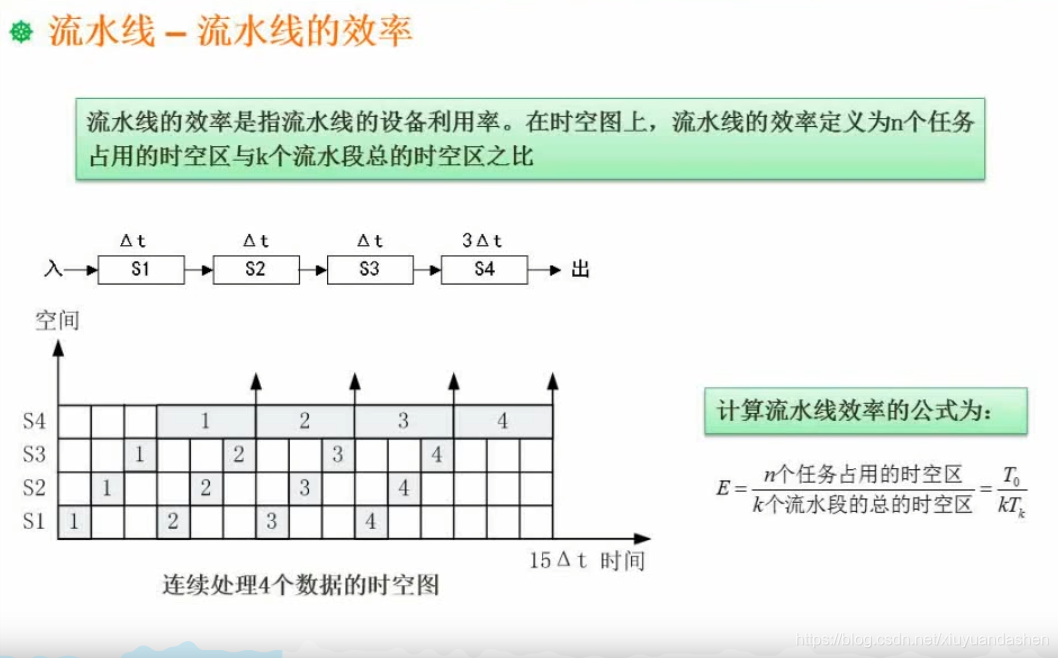
计算机层次化存储结构

Cache的概念

主存的分类

磁盘工作原理

读取磁盘的时候磁头还是会接着旋转的！

计算机的总线

系统可靠性分析与设计

串联系统和并联系统

• 串联系统：只要其中一个环节出现问题，整个系统都不能运行了。
  • 可靠度：把每个环节的可靠度相乘就是总可靠度。
  • 失效率：把每个环节的失效率（1 - 环节可靠度）相加。（近似公式，当子系统比较多，且失效率极低的情况下使用）
  • 
• 并联系统：只要有一个环节不出现问题，系统都可以运行。（当且所有环节故障，才不能运行）

  • 可靠度：1 减去 所有环节失效率之积。

  • 失效率：1 减去 总可靠度

模冗余系统和混合系统

差错控制

校验码的概念

• 检错：检查出错误
• 纠错：检查出错误，并且纠错。
• 码距：例如 11 和 00 ，11要变成00 最少需要变化两个位，所以最小码距为2.
• 

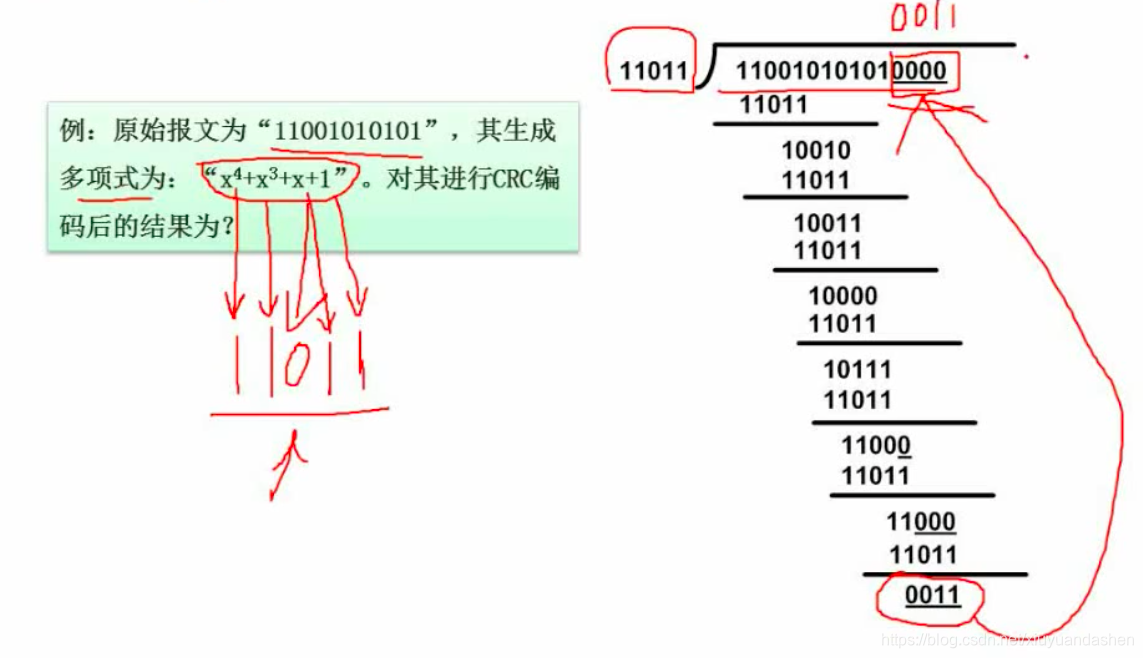
循环（CRC）校验码

可以做检错，但是不可以做纠错的校验码。

• 模2除法： 两个二进制相除时做 异或操作！
• 下图中 x^ 4 +x^3+x+1 ,意思是在 2^ 4、2^3、 2^1 、 2^0 这些位上为1,即 11011 。
• 在原始报文后面添加多项式位数减1个数 的0.
• 然后进行模2除法，将得到余数（对应位数），替换原始报文后添加的0.
• 这样就求出进行CRC编码后的结果。
• 将得到的结果和前面多项式的值11011进行模2除法，如果余数为0则表示对了。
• 

海明校验码

通过 2^r = x+r+1确定校验码为r位（x为信息位的个数），位置为 2^0 ~2^r .

注意： 信息位的位置分配是从高位到低位依次存放

注意： 海明校验码是放在2的幂次位上的

第三步：确定校验位的值

校验原则：被校验的海明位的下标等于所有参与校验该位的校验位的下标之和

然后将校验码校验的信息位的位置记录下来：

r1: 3, 5, 7
r2: 3, 6, 7
r3: 5, 6, 7

然后做对应信息位的异或运算(异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1）)

r1: 1 xor 1 xor 1 = 1
r2: 1 xor 0 xor 1 = 0
r3: 1 xor 0 xor 1 = 0

代入表格得到

注意：按照从低位到高位的排列顺序得到海明码：1010101