本文共 2859 字，大约阅读时间需要 9 分钟。

思路

好像是数论+记忆化搜索？
把子树分成有父亲（A）和无父亲（B）两种情况，这两种情况的删除顺序应该是不相同的。
首先，我们来讨论一下prufer编码（这个太长了，把他简称“P”好了）的总和。
我们把以编号$x$为根，深度为$k$的P的和记为$f_x(k)$。设$f_x(k)=a_kx+b_k+c_k(x\ div \ 2)$，那么：

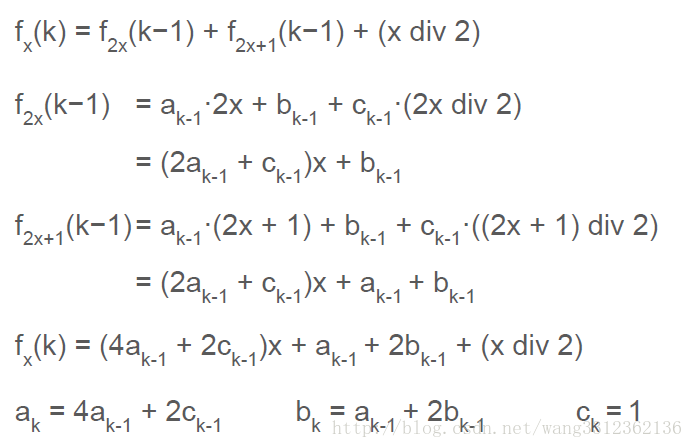
做到这里，我们发现：原来$a_k,b_k,c_k$都是可以递归的！
类似的，我们记录$g_x(k,i)$表示$x$为根，$k$层，已经删了$i$个点的题目中要求的答案。
同样的，可以得到：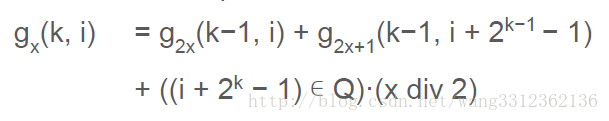

这里也可以递归来求。
但是，如果直接递归求解，时间复杂度会很高，大概是$O(2^k)$的。
所以，我们需要一些技巧：
如果没有询问落在一个区间内，那么这个区间不去递归，而是直接返回0；
否则，记忆化一些状态。
具体来说，就是记录：
1. 深度小于$k\ div\ 2$；
2. 这个区间落在$[a,a+(m-1)d]$内。
记忆化的关键字在代码中讲，递归的方式也在代码中讲。
另外，答案采用多项式的方式保存，最终输出时计算一下多项式的值。

代码

#include <cstdio>#include <algorithm>const int maxm=15;struct data//保存答案：ax+b+c(x div 2){  long long a,b,c;  data(long long a_=0,long long b_=0,long long c_=0)  {    a=a_;    b=b_;    c=c_;  }};data res[maxm+1][1<<maxm];int lm[maxm+1][1<<maxm],nowcase;//lm记录最后一次记忆化是哪一次询问，res记录记忆化结果inline int addleft(data& par,data son)//par加上son的答案，其中son是par的左儿子{  par.a+=2*son.a+son.c;  par.b+=son.b;  return 0;}inline int addright(data& par,data son)//par加上son的答案，其中son是par的右儿子{  par.a+=2*son.a+son.c;  par.b+=son.a+son.b;  return 0;}data search(int deep,int nextq,int m,int d,int hasparent)/* *这里： *deep是这个点的深度 *nextq代表这个区间的左端点 *记忆化的key值是(deep,nextq) *m是最小能满足nextq+m*d大于(1<<deep)-1的m（大概吧） *d是题目中的 *hasparent决定了是A情况还是B情况 */{  if(deep==1)    {      data ans(0,0,1);      return ans;    }  int size=(1<<deep)-1,mem=(deep<=maxm)&&(hasparent)&&(nextq+m*d>=size);  if(mem&&(lm[deep][nextq]==nowcase))//如果在这次询问中被记忆化了，直接返回值    {      return res[deep][nextq];    }  data sol(0,0,0);//记录答案  int nownext=nextq,sonsize=(1<<(deep-1))-1;  if((nownext<sonsize)&&(m>0))//如果这个左子树有对答案产生贡献的点    {      int deltam=std::min(m,(sonsize-nownext-1)/d+1);//求m的变化量，也就是上面说的m值      addleft(sol,search(deep-1,nownext,deltam,d,1));//将左边的答案加入这个的答案      m-=deltam;      nownext+=deltam*d;//防止nownext到达负数    }  nownext-=sonsize;  if(!hasparent)//如果时B类型的子树，删完左边后需要删根，然后删右边    {      if((!nownext)&&(m>0))//如果这个点对答案产生贡献，则计算答案        {          nownext+=d;          --m;          sol.a+=2;          ++sol.b;        }      --nownext;    }  if((nownext<sonsize)&&(m>0))//如果右子树有对答案产生贡献的点    {      int deltam=std::min(m,(sonsize-nownext-1)/d+1);//这一部分和左子树基本相同      addright(sol,search(deep-1,nownext,deltam,d,hasparent));      m-=deltam;      nownext+=deltam*d;    }  nownext-=sonsize;  if(hasparent)//A类型的子树，需要先计算完左右子树，再计算根    {      if(m>0)      //如果可以对答案产生贡献，就增加答案      //这里如果m>0，代表nextq一定为0了，否则m还可以继续减小至0，不符合“最小”的条件        {          ++sol.c;        }    }  if(mem)//记忆化一下答案    {      lm[deep][nextq]=nowcase;      res[deep][nextq]=sol;    }  return sol;}int n,q,a,m,d;int main(){  scanf("%d%d",&n,&q);  while(q--)    {      ++nowcase;      scanf("%d%d%d",&a,&d,&m);      data ans=search(n,a-1,m,d,0);//计算答案多项式，这里a-1是由于根节点的编号为1      printf("%lld\n",ans.a+ans.b);//计算x为1时的答案多项式的值    }  return 0;}