
200116(最短路径的Dijkstra算法(贪心))
发布日期:2021-05-04 06:33:49
浏览次数:31
分类:技术文章
本文共 2943 字,大约阅读时间需要 9 分钟。
本质就是贪心算法。
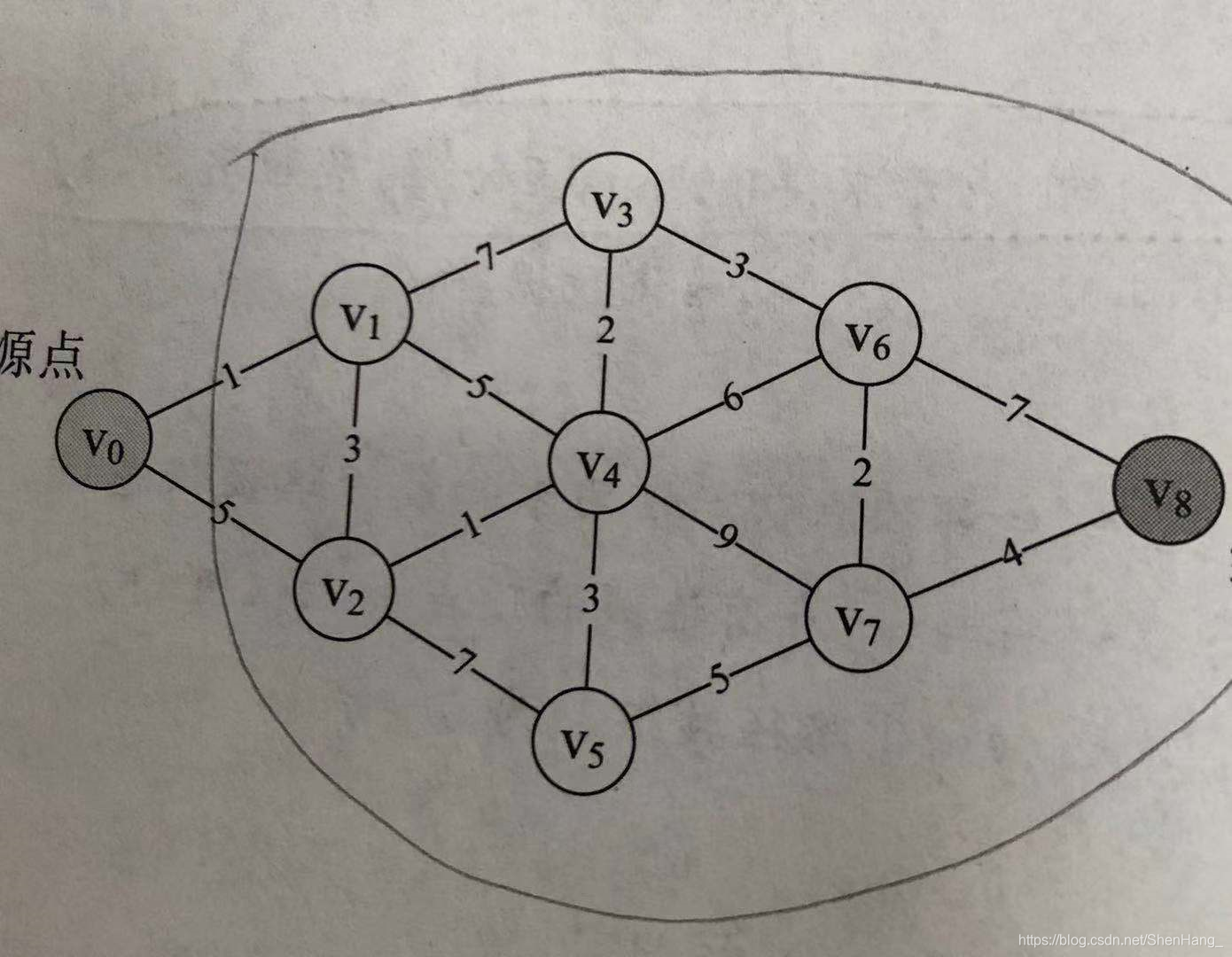
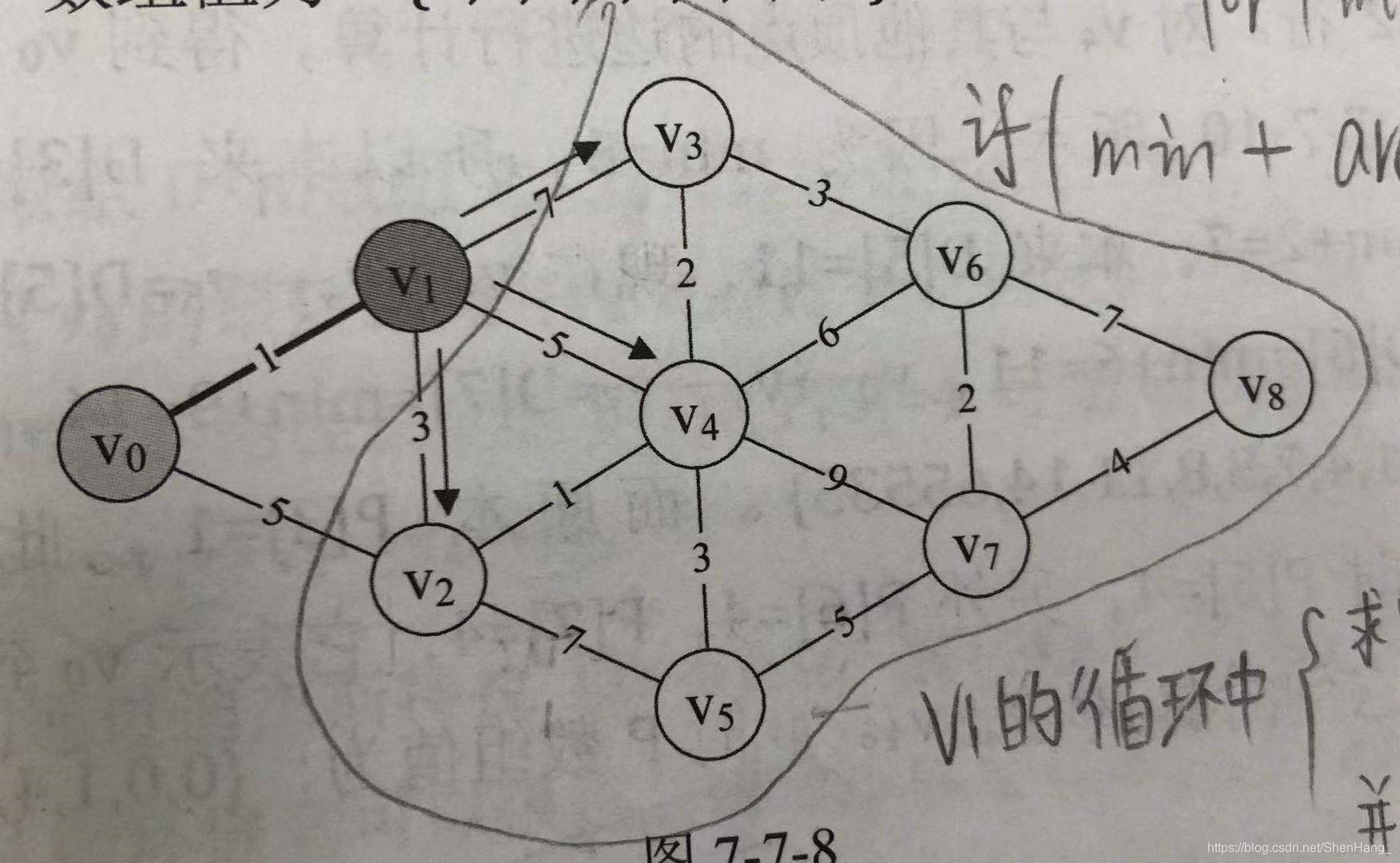
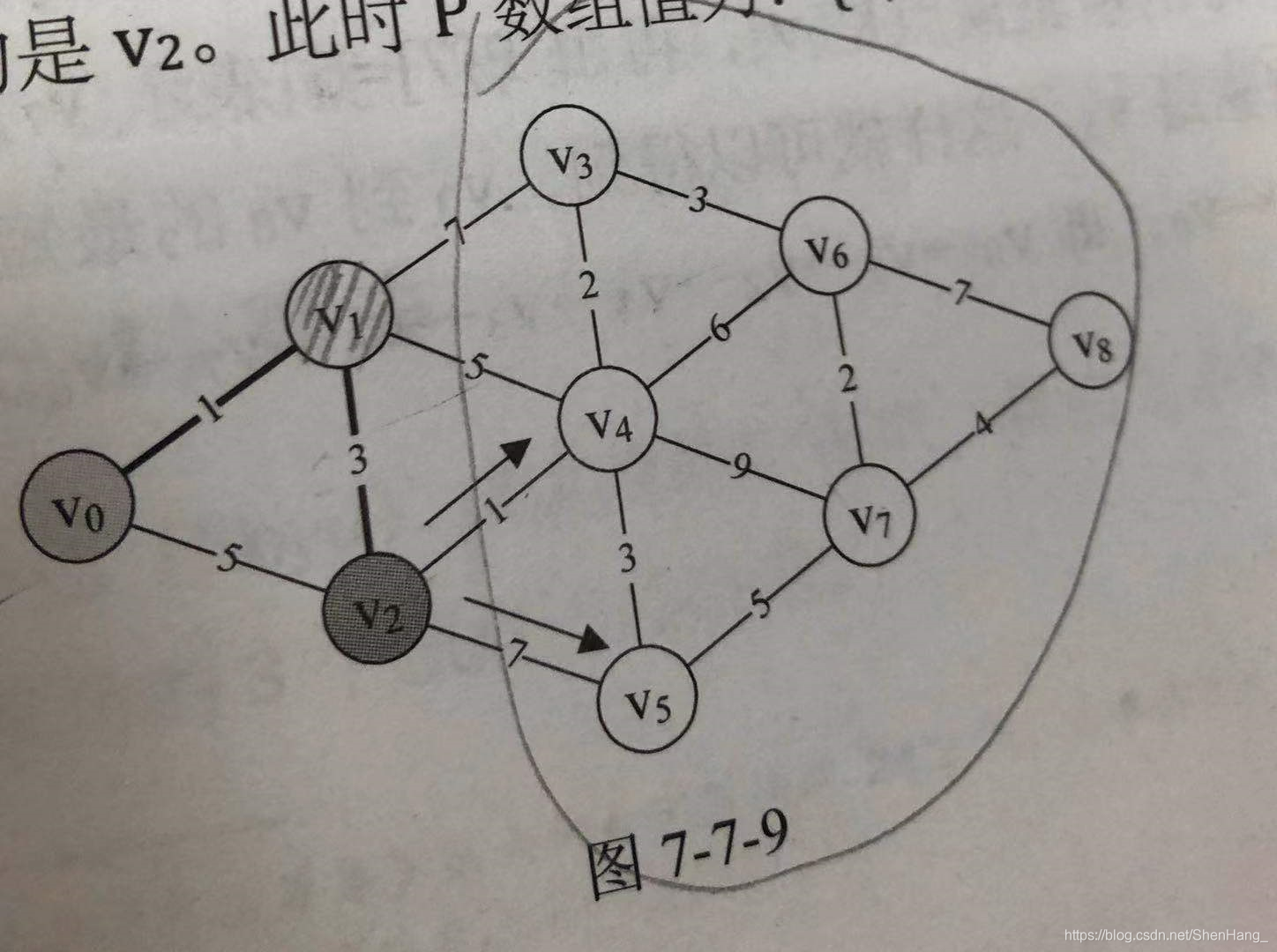
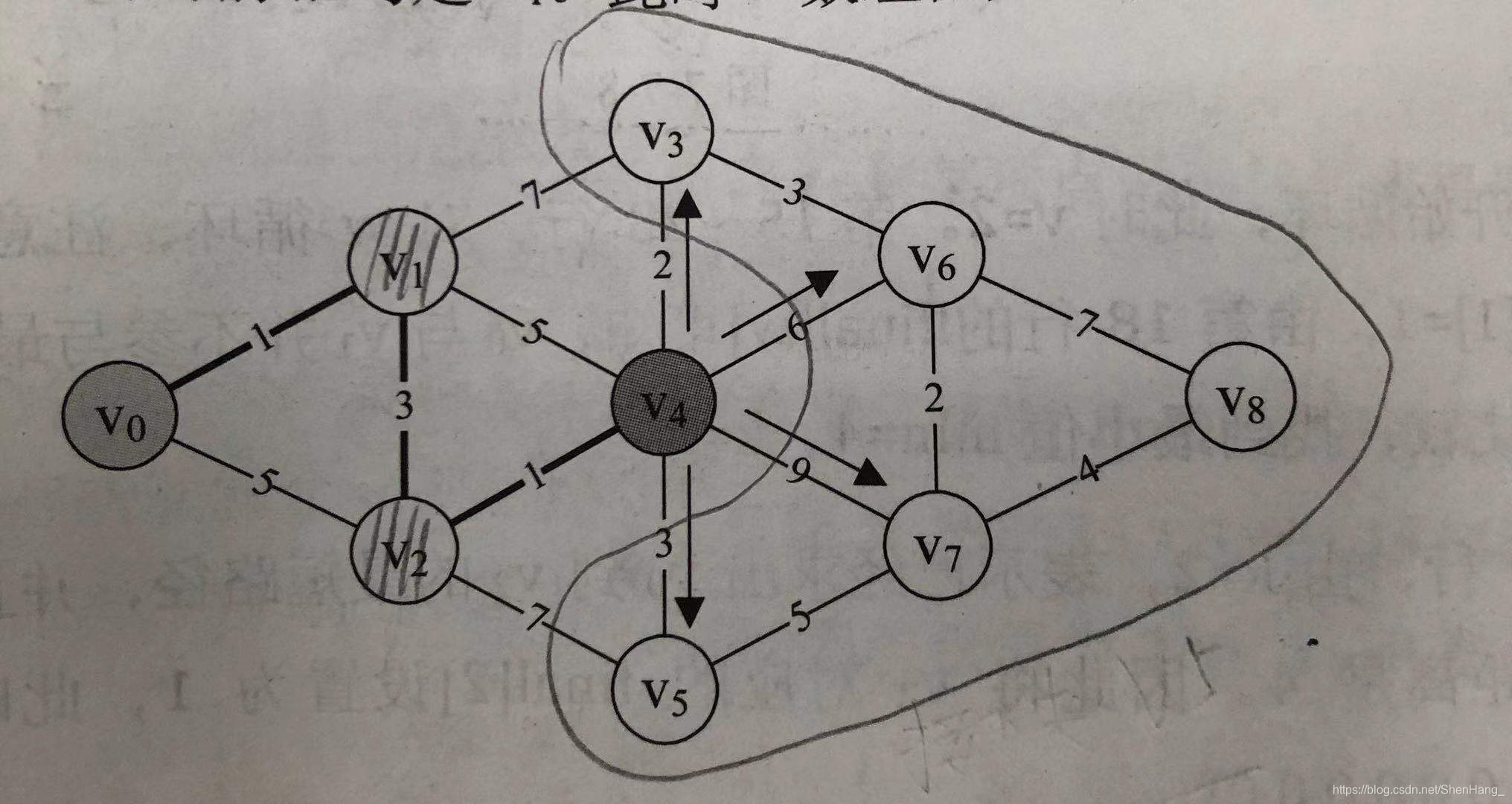
核心思想:基于已经求出的最短路径的基础上,求得更远顶点的最短路径。 P数组:用来记录前驱顶点,如P[8]=6表示v8的前驱顶点是v6; D数组:D[i]表示vi和v0的最短距离; 在每次大循环内: 1.在D数组中找出当前离v0最近的顶点vk(vk是在所有还未被确定最短路径的顶点中选出。因为已经被确定最短路径的顶点和v0的距离已经是最短的了,而且是必定不会改变的),并在flag数组中把下标为k的元素置1; 2.在已经找到v0与vk的最短路径的基础上,对和vk直接相连的且未被确定的顶点进行计算,得到v0与它们的当前距离,并对D数组、和P数组进行修正。 大循环结束后,flag数组全为1,表明所有的顶点都完成了最短路径的查找工作,即v0到任何一个顶点的最短路径都已经被求出。特点:对于每次循环确定的vk,v0与vk的距离是不断增加的。




#includeusing namespace std;#define MAXVEX 9#define INFINITY 65536typedef struct { int arc[MAXVEX][MAXVEX];//邻接矩阵 int numVEXS;//顶点个数}MGraph;void ShortestPath_Dijkstra(MGraph&G);int main() { MGraph G; G.numVEXS = 9; for (int i = 0; i < G.numVEXS; i++) for (int j = 0; j < G.numVEXS; j++) { if (i < j) G.arc[i][j] = INFINITY; if (i == j) G.arc[i][i] = 0; } G.arc[0][1] = 1; G.arc[0][2] = 5; G.arc[1][2] = 3; G.arc[1][3] = 7; G.arc[1][4] = 5; G.arc[2][4] = 1; G.arc[2][5] = 7; G.arc[3][4] = 2; G.arc[3][6] = 3; G.arc[4][5] = 3; G.arc[4][6] = 6; G.arc[4][7] = 9; G.arc[5][7] = 5; G.arc[6][7] = 2; G.arc[6][8] = 7; G.arc[7][8] = 4; for (int i = 0; i < G.numVEXS; i++) for (int j = 0; j < G.numVEXS; j++) { if (i < j) G.arc[j][i] = G.arc[i][j]; } ShortestPath_Dijkstra(G); system("pause"); return 0;}void ShortestPath_Dijkstra(MGraph&G) { int k, min; int D[MAXVEX] = { 0 }, P[MAXVEX] = { 0 }, flag[MAXVEX] = { 0 };//D[v]表示v0到v的最短路径长度和,final[v]=1表示v0到v的最短路径已经被求出,P数组用来最终确定路径用 for (int i = 0; i < G.numVEXS; i++) D[i] = G.arc[0][i]; flag[0] = 1;//v0到v0不需要求最短路径 //start for (int n = 1; n < G.numVEXS; n++) { //开始大循环(次数为G.numVEXS-1) min = INFINITY; for (int i = 0; i < G.numVEXS; i++) { if (!flag[i] && D[i] < min) { min = D[i];//找出当前离v0最近的且未被确定的顶点vk k = i;//记录下标 } } flag[k] = 1;//把顶点vk置为1 //在已经找到v0与vk的最短路径的基础上,对和vk直接相连的且未被确定的顶点进行计算,得到v0与它们的当前距离 for (int i = 0; i < G.numVEXS; i++) { if (!flag[i] && min + G.arc[k][i] < D[i]) //如果找到了更短的路径,则修正D和P { D[i] = min + G.arc[k][i]; P[i] = k;//表示vk是vi的前驱 } } } //打印路径 while (P[k] != k) { cout << P[k] << "-->" << k << endl; k = P[k]; }}
若要求v5到各个顶点的最短路径,只需要修改代码如下:
void ShortestPath_Dijkstra(MGraph&G) { int k, min; int D[MAXVEX] = { 0 }, P[MAXVEX] = { 5,5,5,5,5,5,5,5,5 }, flag[MAXVEX] = { 0 };//D[v]表示v0到v的最短路径长度和,final[v]=1表示v0到v的最短路径已经被求出,P数组用来最终确定路径用 for (int i = 0; i < G.numVEXS; i++) D[i] = G.arc[5][i]; flag[5] = 1;//v5到v5不需要求最短路径 //start for (int n = 1; n < G.numVEXS; n++) { //开始大循环(次数为G.numVEXS-1) min = INFINITY; for (int i = 0; i < G.numVEXS; i++) { if (!flag[i] && D[i] < min) { min = D[i];//找出当前离v5最近的且未被确定的顶点vk k = i;//记录下标 } } flag[k] = 1;//把顶点vk置为1 //在已经找到v5与vk的最短路径的基础上,对和vk直接相连的且未被确定的顶点进行计算,得到v5与它们的当前距离 for (int i = 0; i < G.numVEXS; i++) { if (!flag[i] && min + G.arc[k][i] < D[i]) //如果找到了更短的路径,则修正D和P { D[i] = min + G.arc[k][i]; P[i] = k;//表示vk是vi的前驱 } } } //打印路径 while (P[k] != k) { cout << P[k] << "-->" << k << endl; k = P[k]; }} 发表评论
最新留言
留言是一种美德,欢迎回访!
[***.207.175.100]2025年03月15日 19时31分24秒
关于作者

喝酒易醉,品茶养心,人生如梦,品茶悟道,何以解忧?唯有杜康!
-- 愿君每日到此一游!
推荐文章
腾讯终于要杀入电商直播了
2019-03-03
花1亿扶持优质红人,如涵推动网红经济出圈之路有何深意?
2019-03-03
AMD、Intel、NVIDIA芯片三巨头内战
2019-03-03
颜值经济转向身材经济,医美的第二曲线来了
2019-03-03
开门红财报下,贝壳找房的春天依然有点冷
2019-03-03
B站财报:内容与商业的艰难抉择
2019-03-03
虾米逝去:透视在线音乐的下一场战争
2019-03-03
抢滩抖音、B站,快手港股IPO进程加速
2019-03-03
智能穿戴的结局依然充满悬念
2019-03-03
Linux中的虚拟内存机制和内存映射
2019-03-03
Android系统启动系列5 SystemServer进程下
2019-03-03
Android四大组件系列9 ContentProvider原理
2019-03-03
理解PendingIntent
2019-03-03
Android SurfaceFlinger4 提交Buffer
2019-03-03
深入理解 ClientLifecycleManager 机制
2019-03-03
android基础知识回顾--ContentProvider简单用法
2019-03-03
压缩解压
2019-03-03
js try{}catch(){}finally{}语句
2019-03-03
ES6 块级绑定(二)
2019-03-03
ES6 函数模块(四)
2019-03-03