7 支持向量机

发布日期：2021-06-29 18:41:03 浏览次数：3 分类：技术文章

本文共 9678 字，大约阅读时间需要 32 分钟。

文章目录

是一种二类分类模型.

定义在特征空间上的间隔最大的线性分类器,
- 间隔最大使它有别于感知机

核技巧使它成为实质上的非线性分类器

学习策略就是闾隔最大化,
- 可化为求解凸二次规划,
- 也等价于正则化的合页损失函数的最小化问题
- 学习算法是求解凸二次规划的最优化算法

由简至繁
- 线性可分支持向量机
- 线性支持向量机及非线性支持向量机

训练数据线性可分时,通过硬间隔最大化,学习一个线性分类器,
- 即线性可分支持向量机,又称硬间隔支持向量机

近似线性可分时,通过软间隔最大化,也学习ー个线性的分类器,
- 即线性支持向量机,又称软间隔支持向量机

不可分时,通过核技巧及软间隔最大化,学习非线性支持向量机

输入空间为欧氏空间或离散集合、特征空间为希尔伯特空间时,
- 核函数表示将输入
  - 从输入空间
  - 映射到
  - 特征空间得到的特征向量之间的内积

通过使用核函数可学习非线性支持向量机
- 等价于隐式地在高维的特征空间中学习线性支持向量机
- 这样的方法称为核技巧
- 核方法是比支持向量机更为一般的机器学习方法

Cortes与 Vapnik提出线性支持向量机,

Boser、 Guyon与 Vapnik又引入核技巧,提出非线性支持向量机,

本章按照上述思路介绍3类支持向量机、核函数及一种快速学习算法一一序列最小最优化算法(SMO)

7.1线性可分支持向量机与硬间隔最大化

7.1.1线性可分支持向量机

考虑一个二类分类.

设输入空间与特征空间为两个不同的空间.

输入空间为欧氏空间或离散集合,

特征空间为欧氏空间或希尔伯特空间.

线性可分支持向量机、线性支持向量机假设这两个空间的元素一一对应,并将输入空间中的输入映射为特征空间中的特征向量.

非线性支持向量机利用一个从输入空间到特征空间的非线性映射将输入映射为特征向量、所以,输入都由输入空间转换到特征空间,支持向量机的学习是在特征空间进行的

给定一个特征空间上的训练数据集

$T=\{(x_1,y_1),(x_2,y_2,...,(x_N,y_N))\}$

(x1,y1),(x2,y2,...,(xN,yN))}

设训练数椐集是线性可分

学习目标是在特征空间中找到一个分离超平面,
- 能将实例分到不同的类
- 分离超平面对应于方程・x+b=0,它由法向量p和截距b决定,
- 可用(wb)来表示
- 分离超平面将特征空间划分为两部分,一部分是正类,一部分是负类.
- 法向量指向的一侧为正,另一侧为负

训练集线性可分时,存在无穷个分离超平面可将两类数据正确分开

感知机用误分类最小的策略,求得分离超平面,这时解有无穷多

线性可分支持向量机用间隔最大化求最优分离超平面,解唯一

定义7.1(线性可分支持向量机)

给定线性可分训练数据集,通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为

在这里插入图片描述

以及相应的分类决策函数

在这里插入图片描述

称为线性可分支持向量机

如图7,1所示的二维特征空间中的分类问题,

“。”表示正例

训练数据集线性可分,这时有许多直线能将两类数据正确划分

线性可分支持向量机对应着将两类数据正确划分并且间隔最大的直线

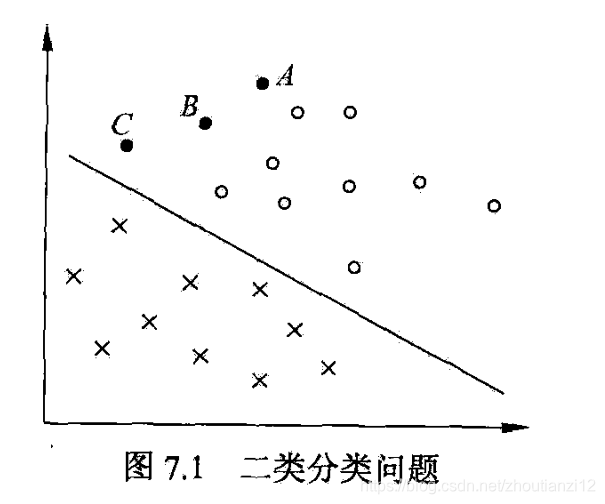
在这里插入图片描述

间隔最大及相应的约束最优化问题在下面叙述.

这里先介绍函数间隔和几何间隔

7.1.2函数间隔和几何间隔

点距分离超平面的远近可表示分类预测的确信程度

超平面确定情况下, $|w\cdot x+b|$ 能表示点 $x$ 距离超平面的远近
- $w\cdot x+b$ 的符号与类标记 $y$ 的符号是否一致能表示分类是否正确,
- 所以可用 $y(w\cdot x+b)$ 表示分类的正确性及确信度,
  - 这是函数间隔

定义7.2(函数间隔)

对给定的训练数据集和超平面

超平面关于样本点的函数间隔为

在这里插入图片描述

超平面关于训练数据集的函数间隔
- 为超平面关于所有样本点的函数间隔之最小值,

在这里插入图片描述

函数间隔可表示分类预测的正确性及确信度.

但选择分离超平面时,只有函数间隔还不够.

因为只要成比例地改变 $w$ 和 $b$ ,如改为 $2 w$ 和 $2 b$
- 超平面并没变,但函数间隔却为原来的2倍

可对法向量 $w$ 加某些约東,如规范化, $∣ ∣ w ∣ ∣ = 1$
- 使间隔是确定的,这时函数间隔成为几何间隔

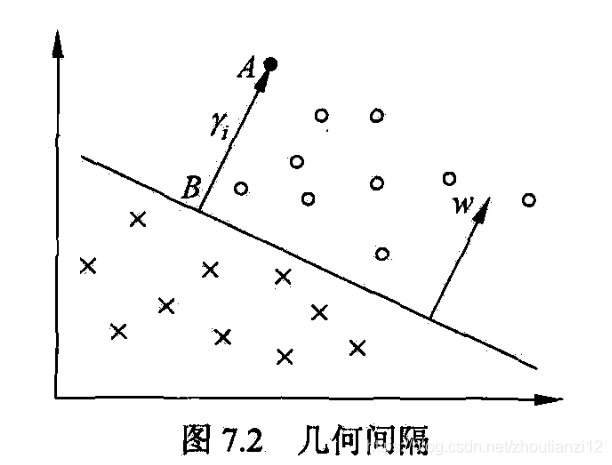
在这里插入图片描述

图7.2给出超平面及其法向量.

点A表某实例 $x_i$ ,类标记为+1

点A与超平面的距离由线段AB给出

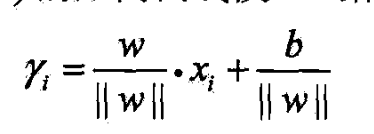
在这里插入图片描述

这是点A在超平面正的一侧的情形.

如果点A在超平面负侧,那么点与超平面的距离为

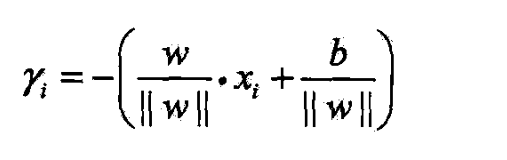
在这里插入图片描述

当样本点被超平面正确分类时,

点 $x_i$ 与超平面的距离是

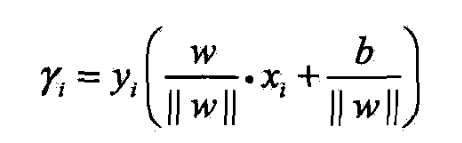
在这里插入图片描述

由这一事实导出几何间隔的概念

定义7.3(几何间隔)

对给定的训练数据集和超平面,

超平面关于样本点的几何间隔为

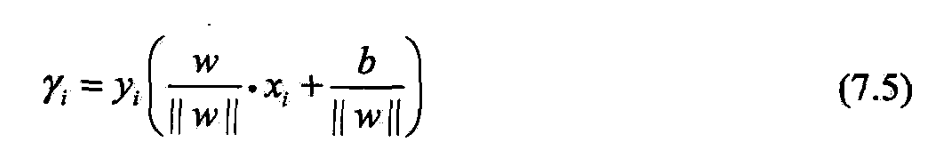
在这里插入图片描述

定义超平面关于训练数据集的几何间隔为超平面关于所有样本点的几何间隔之最小值

在这里插入图片描述

超平面关于样本点的几何间隔一般是实例点到超平面的带符号
的距离,
- 当样本点被超平面正确分类时就是实例点到超平面的距离

函数间隔和几何间隔有下面的关系

在这里插入图片描述

如果咋样,函数间隔和几何间隔相等.

如果 $w$ 和 $b$ 成比例改变(超平面没变)
- 函数间隔也按此比例改变,而几何间隔不变

7.1.3间隔最大化

求解能够正确划分训练集且几何间隔最大的分离超平面

对线性可分的训练数据集而言,
- 线性可分分离超平面有无穷多个(等价于感知机),
- 但几何间隔最大的分离超平面唯一

这里的间隔最大化又称硬间隔最大化(与将要讨论的训练数据集近似线性可分时的软间隔最大化相对应)

间隔最大化直观解释是:
- 对训练集找到几何间隔最大的超平面意味以充分大的确信度对训练数据分类
- 也就是,不仅将正负实例点分开,且对最难分的实例点(离超平面最近的点)也有足够大的确信度将它们分开
- 这样的超平面应该对未知的新实例有很好的分类预测能力

1.最大间隔分离超平面

如何求一个几何间隔最大的分离超平面
- 即最大间隔分离超平面

可表示为

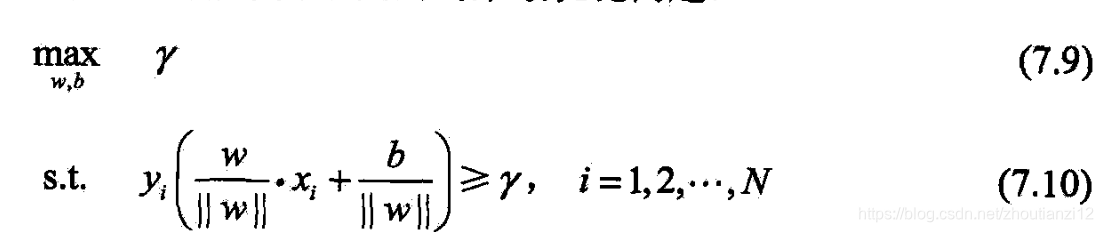
在这里插入图片描述

即我们希望最大化超平面 $(w, b)$ 关于训练数据集的几何间隔 $\gamma$ ,

约束条件表示
- 超平面关于每个训练样本点的几何间隔至少 $\gamma$

几何间隔和函数间隔关系式(7.8)

将这问题改为

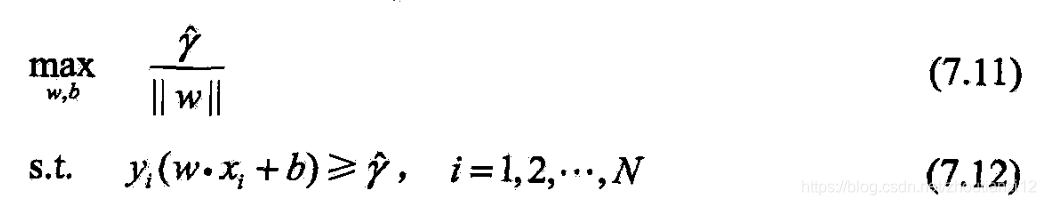
在这里插入图片描述

函数间隔的取值不影响问题的解

设将 $w$ 和 $b$ 改为 $\lambda w$ 和 $\lambda b$ ,这时函数间隔成为
- $\lambda \hat{\gamma}$

函数间隔的这一改变对上面最优化问题的不等式约束没影响,
- 对目标函数的优化也没影响,
- 它产生一个等价的最优化问题

取 $\gamma=1$
- 代入上面最优化
- 注意到最大化啥和最小化啥是等价的,
- 就有

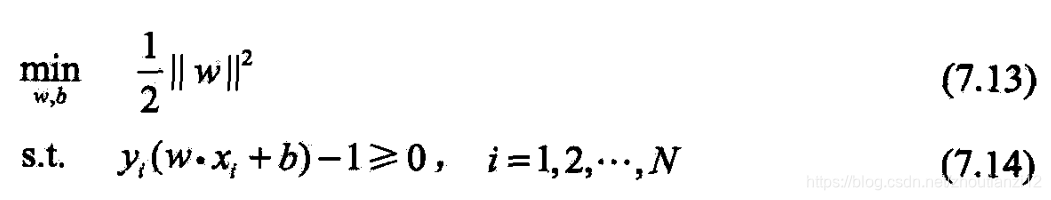
在这里插入图片描述

这是个convex quadratic programming问题

凸优化问题指

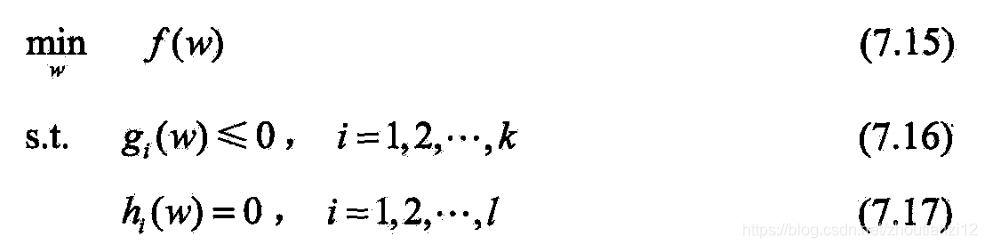
在这里插入图片描述

目标函数和约束函数都是凸函数

仿射函数

当目标函数 $f (w)$ 是二次函数且约束函数 $g_i(w)$ 是仿射函数

上述凸最优化问题成为凸二次规划

如果求出(7.13)~(7.14)的解

那么就可以得到最大间隔分离超平面
- 及
- 分类决策函数
- 即线性可分支持向量机模型

算法7.1

(线性可分支持向量机学习算法最大间隔法)

输入:线性可分训练数据集其中

输出:最大间隔分离超平面和分类决策函数

(1)构造并求解约束最优化问题

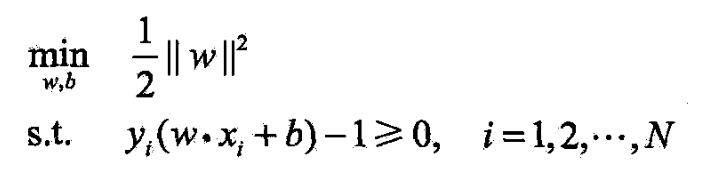
在这里插入图片描述

(2)由此得到分离超平面

分类决策函数

2.最大间隔分离超平面的存在唯一性

3.支持向量和间隔边界

7.1.4学习的对偶算法

为求解(7.13)~(7.14),将它作为原始最优化问题,

用拉格朗日对偶性,

通过求解对偶问题得到原始问题最优解,这就是线性可分支持向量
机的对偶算法.

优点,
- 一是对偶问题往往更容易求解
- 二是自然引入核函数,进而推广到非线性分类问题

先构建拉格朗日函数.

对每一个不等式约束(7.14)

引进拉格朗日乘子

定义拉格朗日函数:

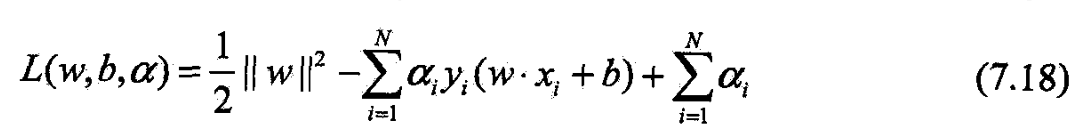
在这里插入图片描述

$\alpha=(\alpha_1,\alpha_2\cdots,\alpha_N)^T$
- 为拉格朗提乘子向量

根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题

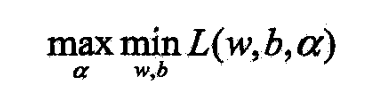
在这里插入图片描述

需先求L对谁的极小,再求对 $\alpha$ 的极大

对 $w$ , $b$ 求偏导

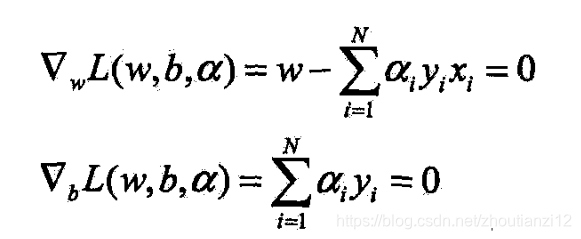
在这里插入图片描述

(7.19)代入拉格朗日函数,并利用(7.20),得

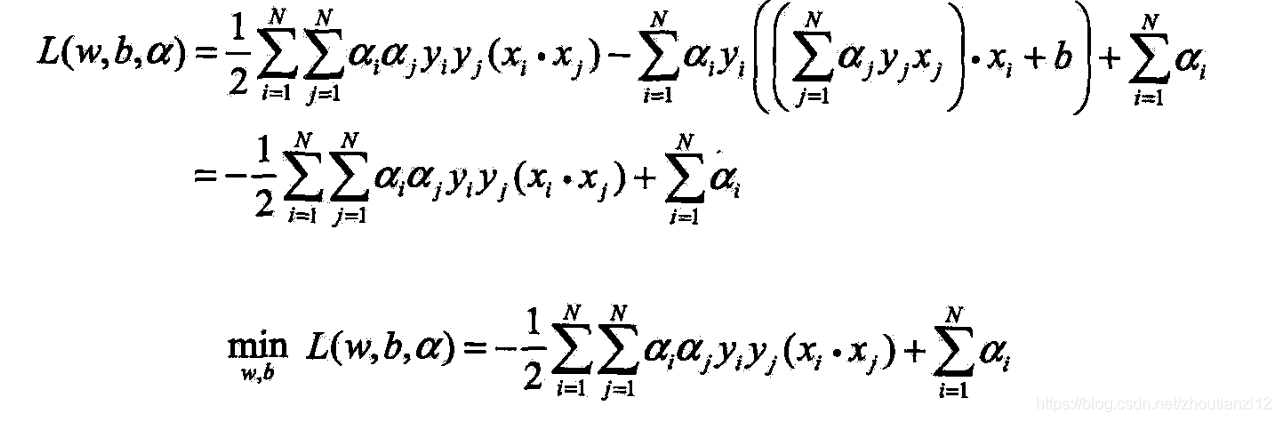
在这里插入图片描述

(2)求 $\min\limits_{w,b}L(w,b,\alpha)$ 对 $\alpha$ 的极大

即是对偶问题

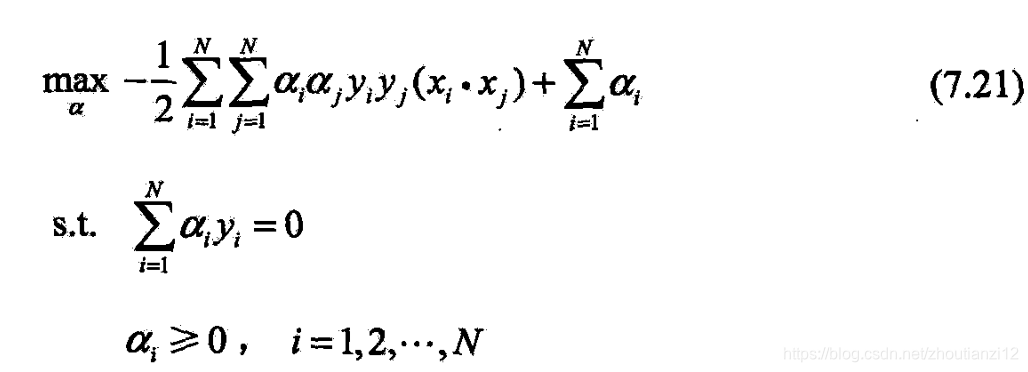
在这里插入图片描述

下面与之等价的对偶最优化

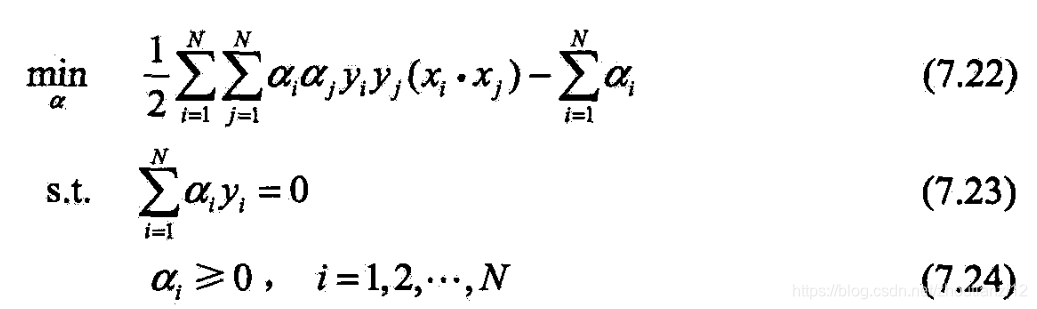
在这里插入图片描述

考虑(7.13)~(7.14)

和(7.22)~(7.24),

原始问题满足定理C.2,

所以存在 $w^*$ , $\alpha^*$ , $\beta^*$ ,使 $w^*$ 是原始问题的解

$\alpha^*$ , $\beta^*$ 是对偶问题的解

(7.13)~(7.14)
- 可转为求(7.22)~(7.24)

对线性可分训练集

设(7.22)~(7.24)对 $\alpha$ 的解为
- $\alpha^*=(\alpha_1^*,\alpha_2^*,\cdots,\alpha_N^*)^T$

由 $\alpha^*$ 求得(7.13)~(7.14)
- 对 $(w, b)$ 的解 $w^*,b^*$
- 有下面定理

定理7.2

设 $\alpha^*=(\alpha_1^*,\alpha_2^*,\cdots,\alpha_N^*)^T$ 是(7.22)~(7.24)的解,

则存在下标 $j$ ,使 $a_j^*>0$ ,并可按下式求得(7.13)~(7.14)的解

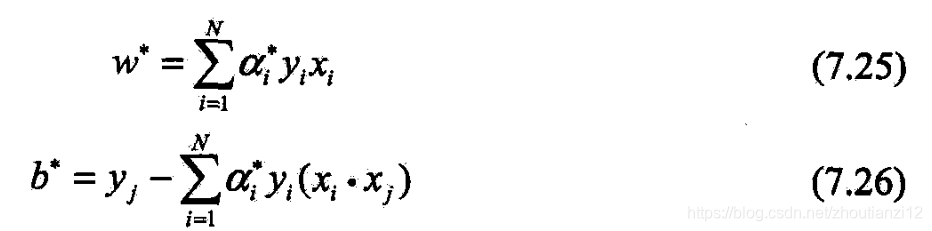
在这里插入图片描述

7.2线性支持向量机与软间隔最大化

7.2.1线性支持向量机

线性可分问题的支持向量机学习方法,对线性不可分训练数据是不适用的,因为这时上述方法中的不等式约束并不能都成立.

怎么オ能将它扩展到线性不可分问题呢?

这就需要修改硬间隔最大化,使其成为软间隔最大化.

给定特征空间上的训练集
- 不线性可分的

有些特异点,将这些特异点除去后,
- 剩下大部分的样本点组成的集合是线性可分

线性不可分意味某些样本点不能满足函数间隔大于等于1的约束
- 可对每个样本点引进一个松弛变量 $\xi_i\ge 0$

使函数间隔加上松弛变量 $\ge 1$

变为

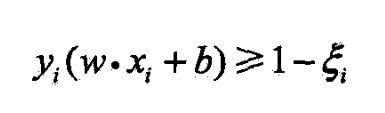
在这里插入图片描述

对每个松弛变量,支付一个代价 $\xi_i$

目标函数变成

在这里插入图片描述

称为惩罚参数,由应用问题决定
- 大时对误分类的惩罚增大
- 小时对误分类的惩罚减小

(7.31)含两层含义
- 使间隔尽量大
- 使误分类点的个数尽量小
- C是调和二者的系数

可和线性可分时一样
- 来考虑不可分时的线性支持向量机学习
- 相应于硬间隔最大化
- 它称软间隔最大化

线性不可分的线性支持向量机变成凸二次规划(原始问题):

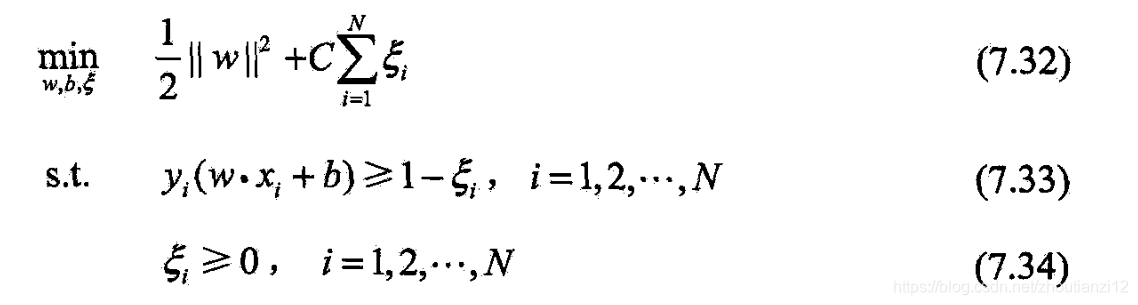
在这里插入图片描述

(7.32)~(7.34)是凸二次规划问题,
- 因而关于 $(w,b,\xi)$ 的解存在
- 可证 $w$ 唯一的,但 $b$ 不唯一, $b$ 存在于一个区间

(7.32)~(7.34)的解是 $w^*$ , $b^*$

于是可得到分离超平面 $w^*\cdot x+b^*=0$ 及分类决策函数

称这样的模型为训练样本线性不可分时的线性支持向量机
- 简称为线性支持向量机

显然,线性支持向量机包含线性可分支持向量机

现实中训练数据集往往线性不可分
- 线性支持向量机有更广的适用性

定义7.5(线性支持向量机)

给定线性不可分数据集,通过求解凸二次规划问题,
- 即软间隔最大化问题(7.32)~(7.34),

得分离超平面

在这里插入图片描述

及相应的分类决策函数

在这里插入图片描述

称线性支持向量机

7.2.2学习的对偶算法

(7.32)~(7.34)的对偶问题是

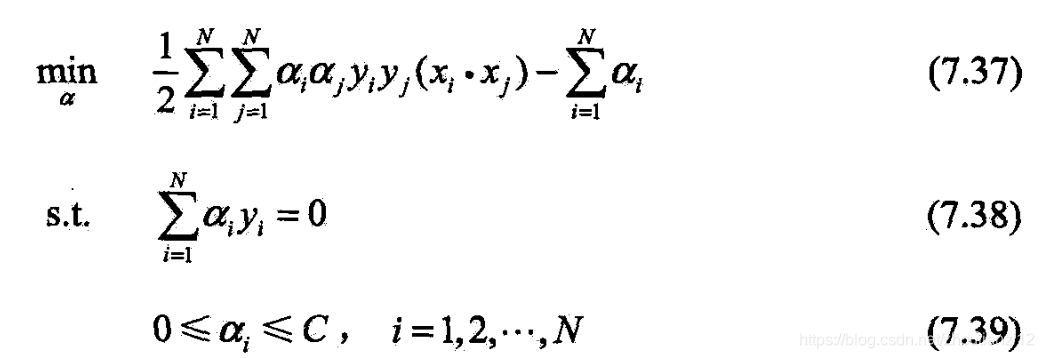
在这里插入图片描述

(7.32)~(7.34)的拉格朗日函数

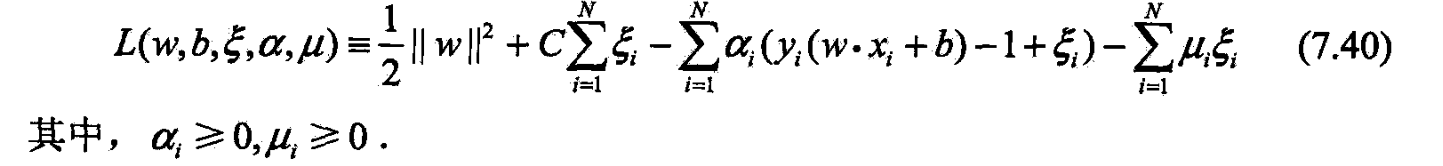
在这里插入图片描述

对偶问题是拉格朗日的极大极小.

先求 $L$ 对 $w,b,\xi$ 的极小

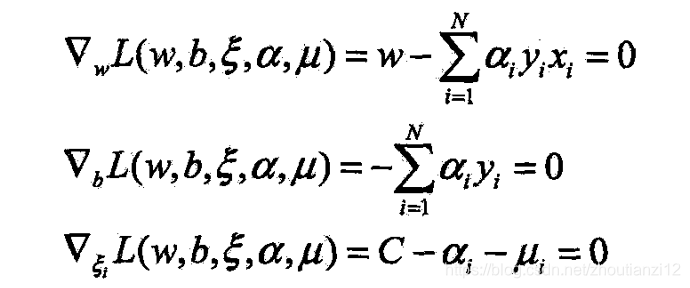
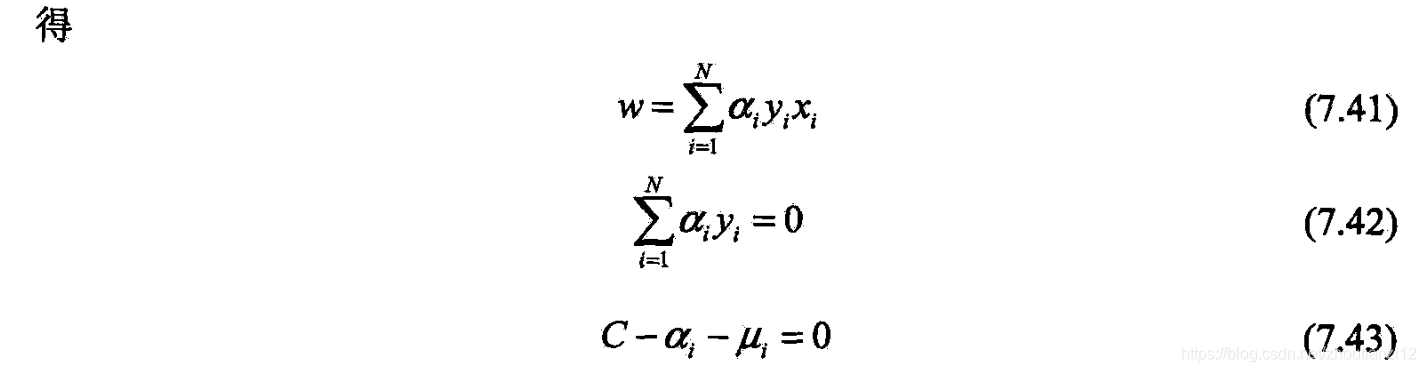
在这里插入图片描述

将(7.41)~(7.43)代入(7.40)

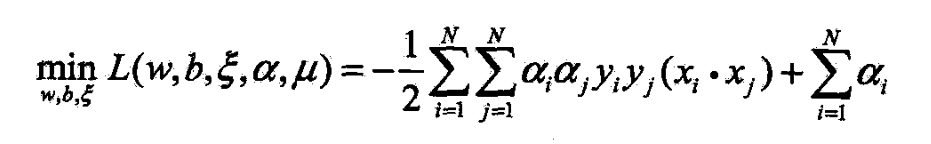
在这里插入图片描述

再对他求极大,即得对偶问题

在这里插入图片描述

将(7.44)~(7.48)变换:用等式约束(7.46)消去 $\mu_i$
- 只留下 $\alpha_i$ ,
- 将(7.46)~(7.48)写成

在这里插入图片描述

再将对目标函数求极大转为求极小
- 得到对偶问题(7.37)~(7.39)

可通过求解对偶问题得到原始问题的解
- 进而确定分离超平面和决策函数

定理7.3

设 $\alpha^*$ 是对偶问题7.37-7.39的一个解

若存在 $\alpha^*$ 的一个分量0< $\alpha_j^*<C$ ,

则(7.32)-(7.34)的解可按下式求

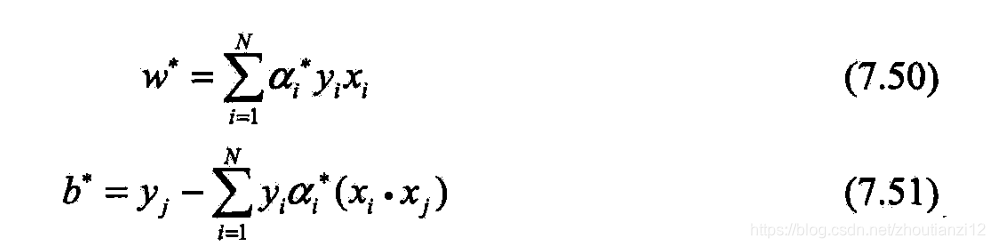
在这里插入图片描述

原始问题是凸二次规划问题,解满足KKT条件

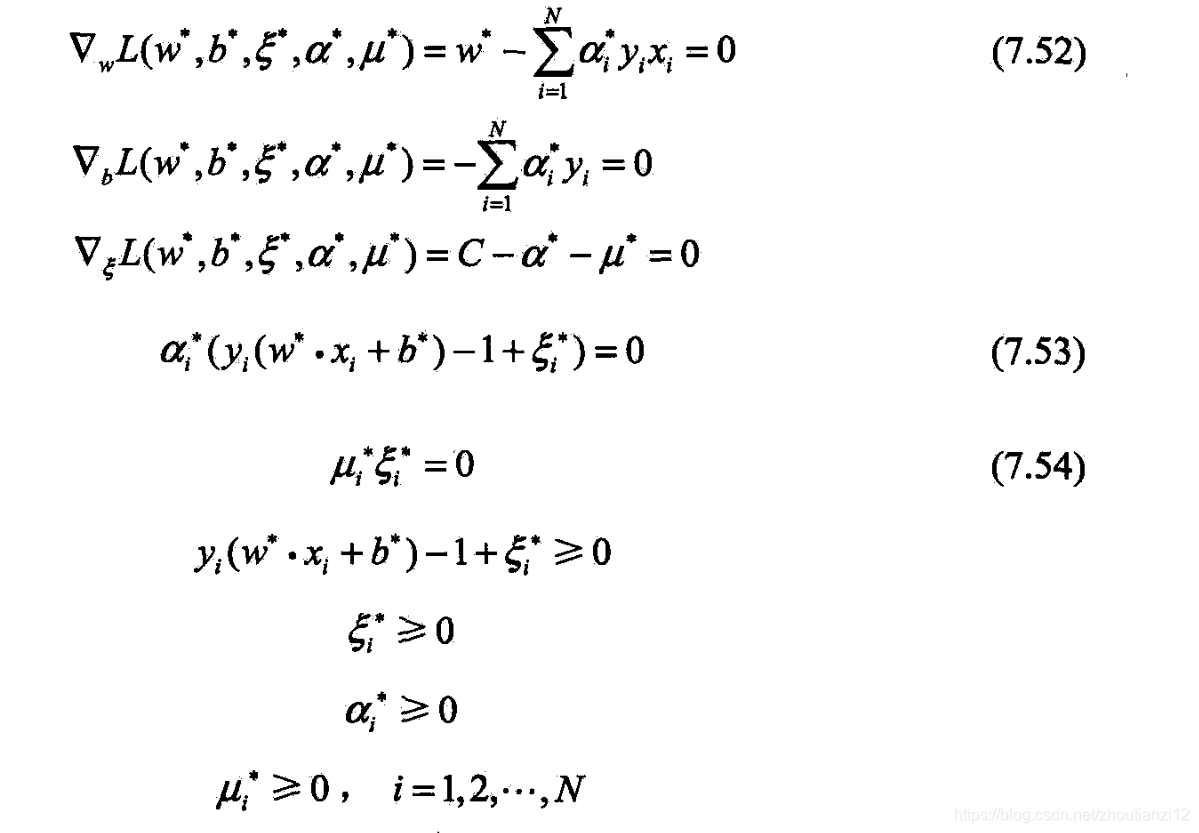
在这里插入图片描述

由(7.52)知(7.50)成立.

再由(7.53)~(7-54知,

若存在 $0<\alpha_j^*<C$ ,

则 $y_i(w^*\cdot x_i+b^*)-1=0$
- 即得(7.51)

分离超平面可写成

在这里插入图片描述

算法7.3

(线性支持向量机学习算法)

输入:训练数据集

输出:分离超平面和分类决策函数
(1)选择惩罚参数C>0,构造并求解凸二次规划问题

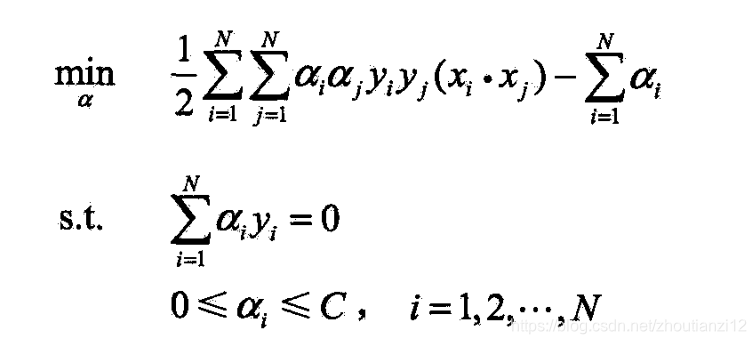
在这里插入图片描述

求得最优解 $\alpha^*$

(2)

计算 $w^*=\sum\limits_{i=1}^N\alpha_i^*y_ix_i$

选择 $\alpha^*$ 的一个分量 $\alpha_j^*$ 适合 $0<\alpha_j^*<C$

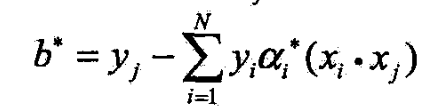
在这里插入图片描述

(3)求得分离超平面,分类决策函数:

步骤(2)中,对任一适合条件的 $\alpha_j^*$

按(7.51)都可求出 $b^*$ ,
- 原始问题(7.32)~(7.34)对 $b$ 的解不唯一
- 实际计算时可取在所有符合条件的样本点上的均值

7.2.3支持向量

线性不可分时,将7.37-7.39的解 $\alpha^*$ 中对应于 $\alpha_i^*>0$ 的样本点的实例 $x_i$ 称支持向量(软间隔的支持向量)

如图7.5

分离超平面实线,间隔边界虚线
- 上面是正例
- 实例元到间隔边界的距离 $\frac{\xi_i}{||w||}$

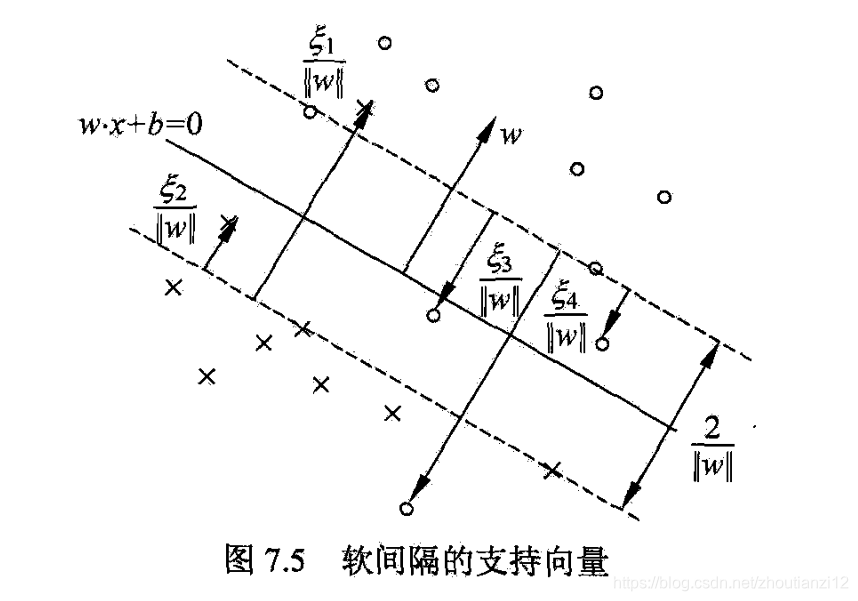
在这里插入图片描述

软间隔的支持向量或在间隔边界上
- 间隔边界与分离超平面之间
- 分离超平面误分一侧

若 $\alpha_i^*<C$ ,则 $\xi_i=0$ ,恰好落在间隔边界上

若 $\alpha_i^*=C$ , $0<\xi_i<1$ ,则分类正确,
- 间隔边界与分离超平面之间:

若 $\alpha_i^*=C$ , $\xi_i=1$ ,在分离超平面上;

若 $\alpha_i^*=C$ , $\xi_i>1$ ,则分离超平面误分一侧

7.2.4合页损失函数

对线性支持向量机,

学习策略为软间隔最大化
- 学习算法为凸二次规划

线性支持向量机学习还有另外一种解释,

最小化

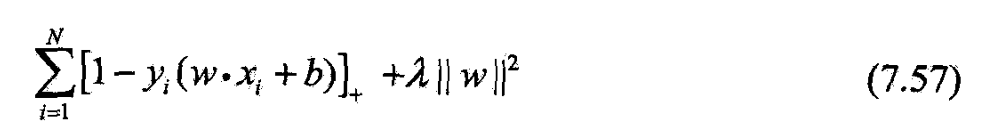
在这里插入图片描述

第1项是经验损失或经验风险

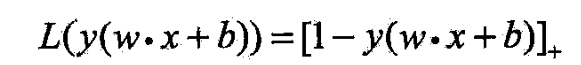
在这里插入图片描述

称合页损失函数

当样本 $x_i,y_i)$ 被正确分类且函数间隔(确信度) $y_i(w\cdot x_i+b)$ 大于1时,损失是0,否则是 $1-y_i(w\cdot x_i+b)$

图7.5的 $x_4$ 被正确分类,但损失不是0

第2项是正则化项

定理7.4

线性支持向量机原始最优化问题

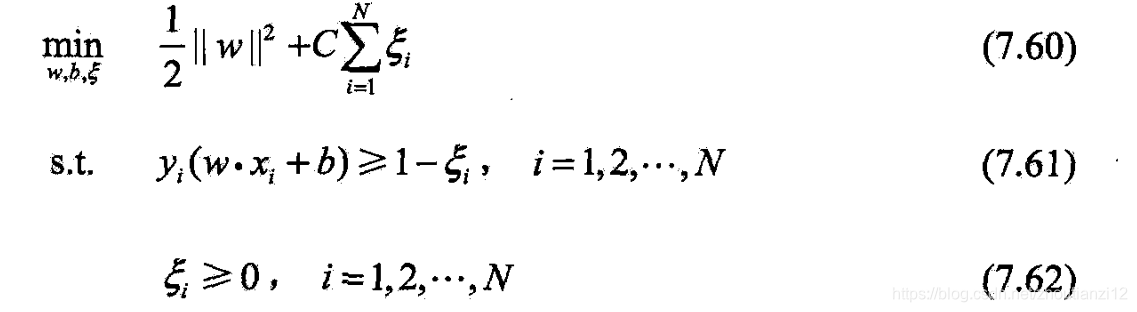
在这里插入图片描述

等价于

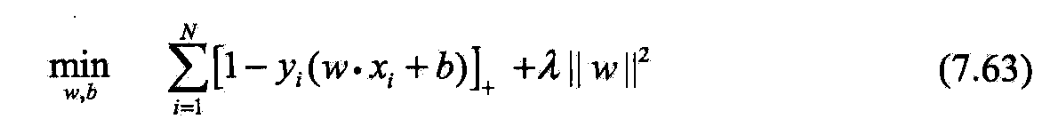
在这里插入图片描述

则 $y_i(w\cdot x_i+b)\ge 1-\xi_i$

于是 $w,b,\xi_i$ 满足约束(7.61)~(7.62).

由(7.64)有

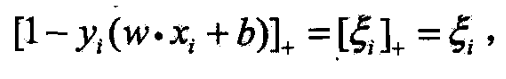
在这里插入图片描述

所以(7.63)可写成

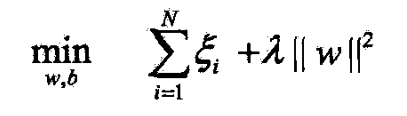
在这里插入图片描述

若取 $\lambda=\frac{1}{2C}$ ,则

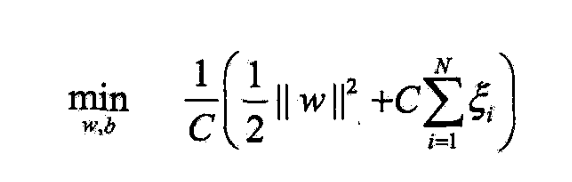
在这里插入图片描述

与(7.60)等价

也可将(7.60)~(7.62)表示成(7.63)

合页损失函数如图7.6,横轴是函数间隔
- 纵轴是损失

像一个合页,故名合页损失函数

还画出0-1损失函数,它是二类分类问题的真正的损失函数,
- 合页损失函数是0-1损失函数的上界
- 0-1损失函数不是连续可导的,直接优化由其构成的目标函数较困难,可认为线性支持向量机是优化由0-1损失函数的上界(合页损失函数)构成的目标函数

这时的上界损失函数又称代surrogate loss function

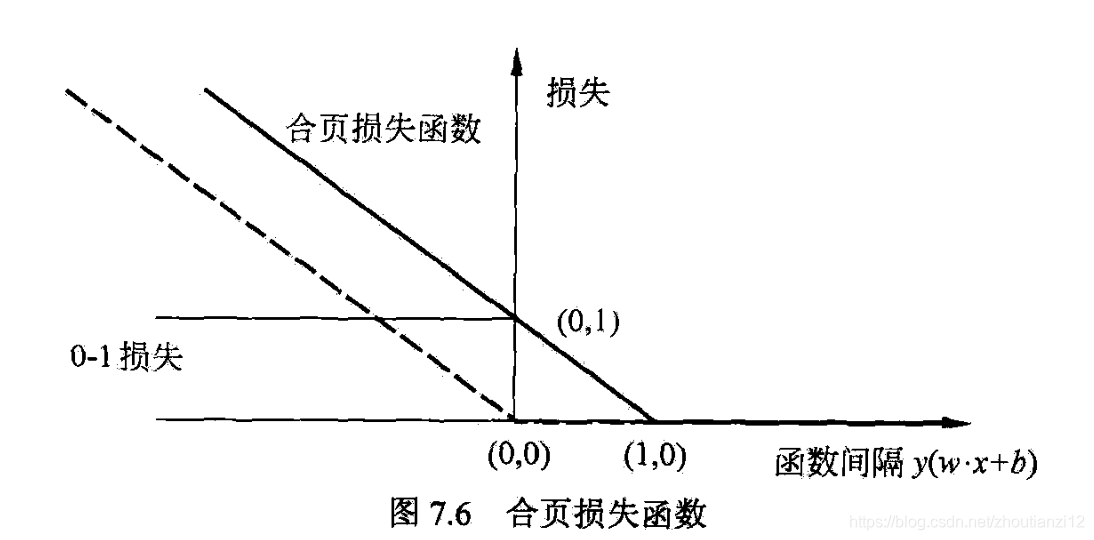
在这里插入图片描述

虚线是感知机的损失函数 $[y_i(w\cdot x_i+b)]_+$ .

这时,当样本点被正确分类时,损失是0,否则是 $-y_i(w\cdot x_i+b)$

合页损失函数不仅要分类正确,且确信度足够高时损失才是0
- 合页损失函数对学习有更高的要求

7.3非线性支持向量机与核函数

本节叙述非线性支持向量机,
- 其主要特点是核技巧.

先要介绍核技巧

核技巧不仅应用于支持向量机,且应用于其他统计学习问题

7.3.1核技巧

1.非线性分类问题

7.7左图

无法用直线将正负实例分开,可用椭圆曲线

对给定的一个训练数据集

实例 $x$ 属于输入空间

如果能用 $R^n$ 中的一个超曲面将正负例正确分开
- 则称这个问题为非线性可分问题

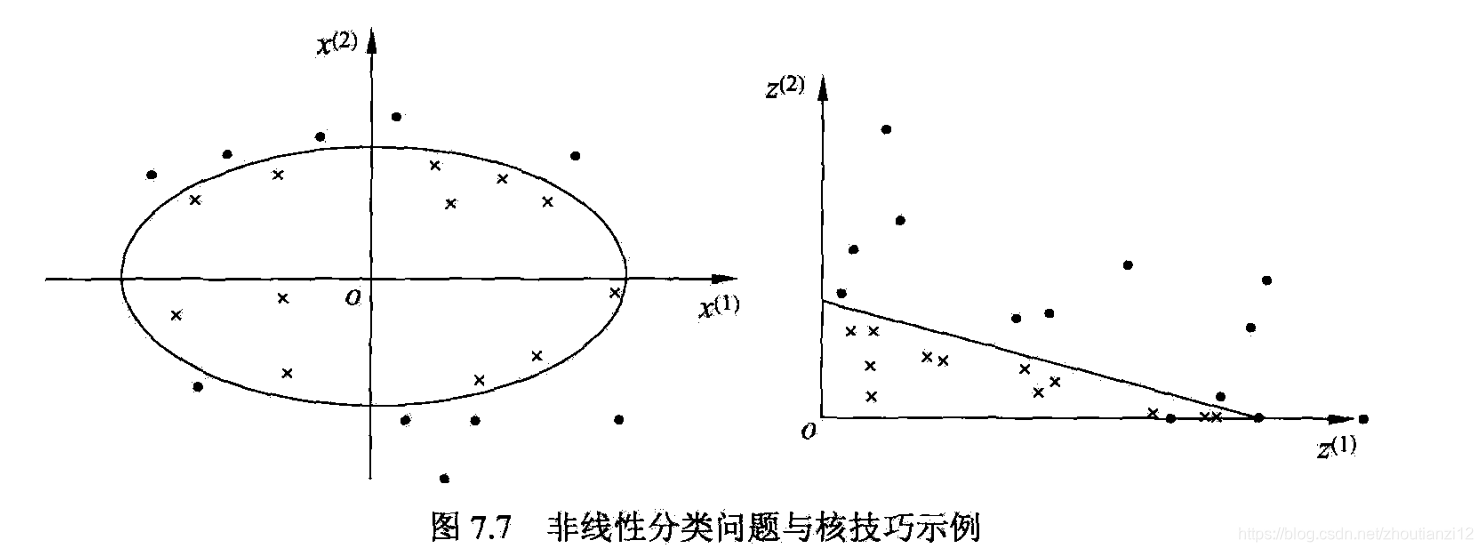
在这里插入图片描述

图7.7

通过变换,将左图中椭圆变成右图直线

原空间为 $R^2$ ,

$x=(x^{(1)},x^{(2)})^T$ ,

$z=(z^{(1)},z^{(2)})^T$

定义从原空间到新空间的变换(映射)

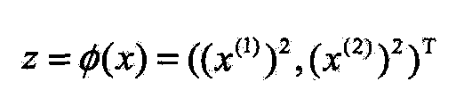
在这里插入图片描述

经过变换 $z=\phi(x)$

原空间变换为新空间,

原空间中的点相应地变换为新空间中的点,

原空间中的椭圆

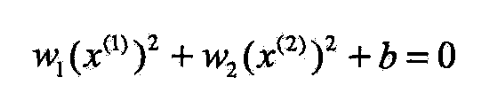
在这里插入图片描述

变换成为新空间中的直线

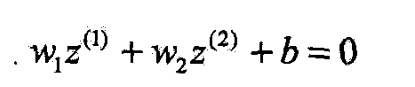
在这里插入图片描述

在变换后的新空间里,直线可将变换后的正负实例点分开

原空间的非线性可分问题就变成了新空间的线性可分问题

线性分类法求解非线性分类分两步
- 用变换将原空间的数据映射到新空间
- 然后新空间里用线性分类学习法从训练数据中学习分类模型
- 核技巧就属这法

核技巧应用到支持向量机
- 通过非线性变换将输入空间(欧氏空间或离散集合)对应
  - 一个特征空间(希尔伯特空间)
- 使输入空间中的超曲面对应特征空间中的超平面
- 分类问题
  - 通过在特征空间中求解线性支持向量机就可完成

2.核函数的定义

定义7.6(核函数)

谁是输入空间(欧氏空间R"的子集或离散集合)

谁为特征空间(希尔伯特空间)

如果存在一个从谁到谁的映射

在这里插入图片描述

使对所有$x,z\in\mathcal{X} $,

$K (x, z)$ 满足

在这里插入图片描述

则称 $K (x, z)$ 为核函数

谁为映射函数

谁为谁和谁的内积

学习与预测中只定义核函数,不显式定义映射函数

直接计算 $K (x, z)$ 较易
- 通过 $\phi(x)$ 和 $\phi(z)$ 计算 $K (x, z)$ 不易

$\phi$ 是输入空间到特征空间的映射
- 特征空间一般高维,甚至无穷维
- 对给定的核 $K (x, z)$ ,
  - 特征空间和映射函数的取法并不唯一
    - 可取不同的特征空间
    - 即便同一特征空间里也可取不同映射

例7.3

设输入空间是 $R^2$ ,核函数是 $K(x,z)=(x・z)^2$

试找出特征空间究和映射

取特征空间 $\mathcal{H}=R^3$

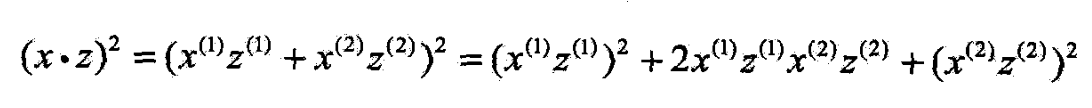
在这里插入图片描述

所以可以取映射

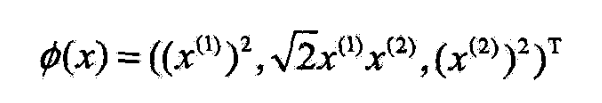
在这里插入图片描述

仍取 $\mathcal{H}=R^3$

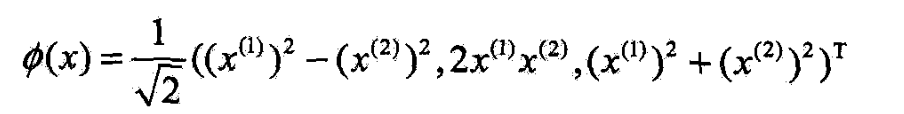
在这里插入图片描述

还可取 $\mathcal{H}=R^4$

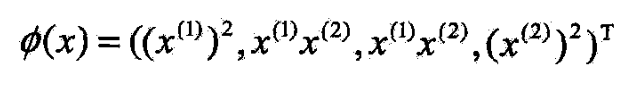
在这里插入图片描述

7.3.2正定核

不用构造映射

能否直接判断一个给定的函数是不是核函数?

$K (x, z)$ 满足什么条件オ能成为核函数?

本节正定核的充要条件.

通常核函数就是正定核函数

为证明此定理先介绍有关的预备知识

设 $K (x, z)$ 是定义在 $\mathcal{X}\times \mathcal{X}$ 上的对称函数,且对任意 $x_1,x_2,...,x_m\in\mathcal{X}$
- $K (x, z)$ 关于 $x_1,x_2,...,x_m$ 的Gram矩阵半正定

可依据函数 $K (x, z)$ ,构成一个希尔伯特空间
- 步骤是:
  - 首先定义映射 $\phi$ 并构成向量空间 $S$
  - 然后在 $S$ 上定义内积构成内积空间;
  - 最后将 $S$ 完备化构成希尔伯特空间

写到这儿了

7.3.3 常用核函数…

7.3.4 非线性支持向量分类机…

7.4 序列最小最优化算法

7.4.1 两个变量二次规划的求解方法

7.4.2 变量的选择方法

7.4.3 SMO算法

本章概要

继续阅读…

转载地址：https://cyj666.blog.csdn.net/article/details/105024526 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！

上一篇：附录C

下一篇：2 Z变换

发表评论

关于作者

喝酒易醉，品茶养心，人生如梦，品茶悟道，何以解忧？唯有杜康！

-- 愿君每日到此一游！

文章目录

7.1线性可分支持向量机与硬间隔最大化

7.1.1线性可分支持向量机

7.1.2函数间隔和几何间隔

7.1.3间隔最大化

1.最大间隔分离超平面

2.最大间隔分离超平面的存在唯一性

3.支持向量和间隔边界

7.1.4学习的对偶算法

7.2线性支持向量机与软间隔最大化

7.2.1线性支持向量机

7.2.2学习的对偶算法

7.2.3支持向量

7.2.4合页损失函数

7.3非线性支持向量机与核函数

7.3.1核技巧

1.非线性分类问题

2.核函数的定义

7.3.2正定核

7.3.3 常用核函数…

7.3.4 非线性支持向量分类机…

7.4 序列最小最优化算法

7.4.1 两个变量二次规划的求解方法

7.4.2 变量的选择方法

7.4.3 SMO算法

本章概要

继续阅读…

发表评论

最新留言

关于作者

推荐文章