本文共 8370 字，大约阅读时间需要 27 分钟。

生活中的图

地图中的图

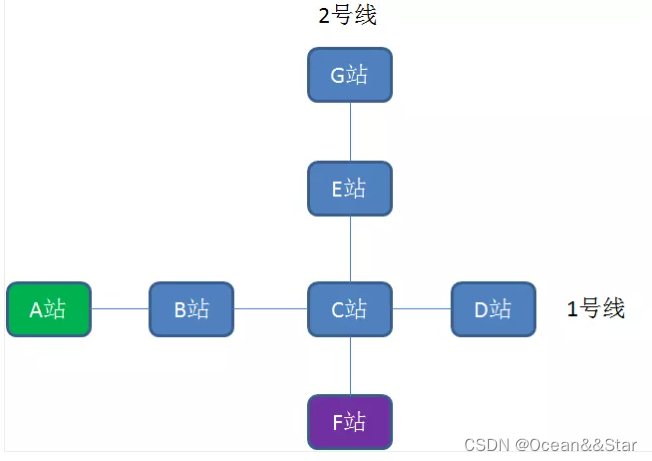
我们在用百度地图的时候，常常会使用导航功能。比如你在地铁站A附近，你想去的地点在地铁站F附近，那么导航就会告诉你一个最佳的地铁线路换乘方案。

这许许多多地铁站所组成的交通网络，也可以认为是数据结构中的图。

社交网络中的图

举个例子，比如微信。假设你的微信朋友圈中有若干好友：张三、李四、王五、赵六、七大姑、八大姨。

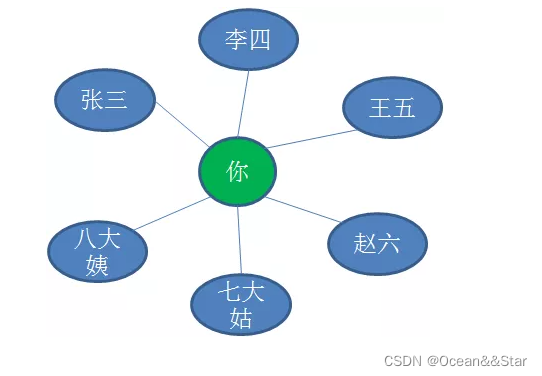
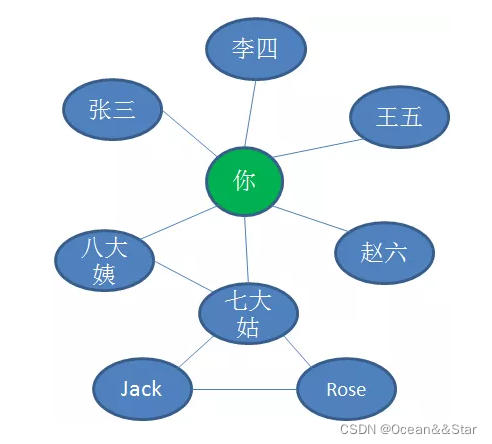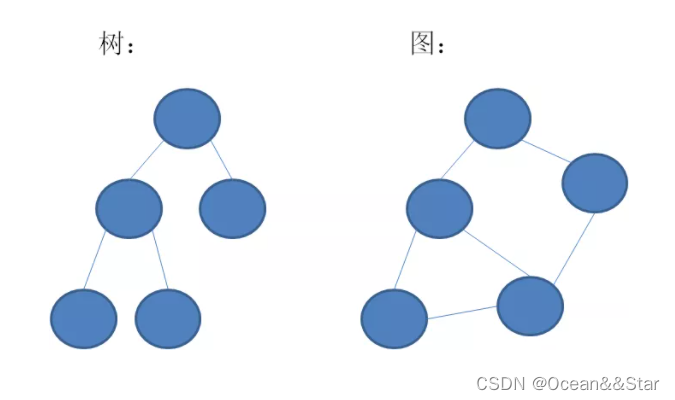
而你七大姑的微信号里，又有若干好友：你、八大姨、Jack、Rose。 微信中，这许许多多的用户就组成了一个多对多的朋友关系网，这个关系网就是数据结构中的图(grahp)。

图，是一种比树更加复杂的数据结构。树的节点之间是一对多的关系，并且存在父与子的层级划分；而图的顶点之间是多对多的关系，并且所有的节点是平等的，无所谓谁是父谁是子。

图

定义

图(graph)是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：$G(V,E)$，其中，G表示一个图，V是图G中顶点（vertex）的集合，E是图G中边（Edge）的集合。

对于图的定义，我们需要明确几个注意的地方：

• 线性表中我们把数据元素叫元素，树中叫结点，在图中数据元素我们则称之为顶点(Vertex)。
• 线性表可以没有数据元素，称为空表，树中可以没有结点，叫做空树，但是，在图中不允许没有顶点，但是可以没有边
• 线性表中，相邻的数据元素之间具有线性关系，树结构中，相邻两层的结点具有层次关系，而图结构中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的。

如下中，共有 V0，V1，V2，V3 这 4 个顶点，4 个顶点之间共有 5 条边。

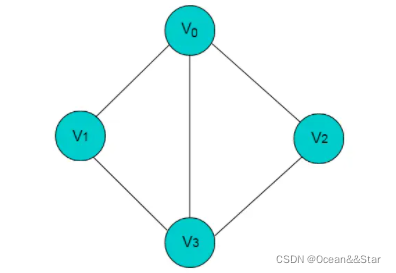
顶点 && 边

在图中，最基本的单元是顶点(vertex)，相当于树中的节点。顶点之间的关联关系叫做边(edge)。

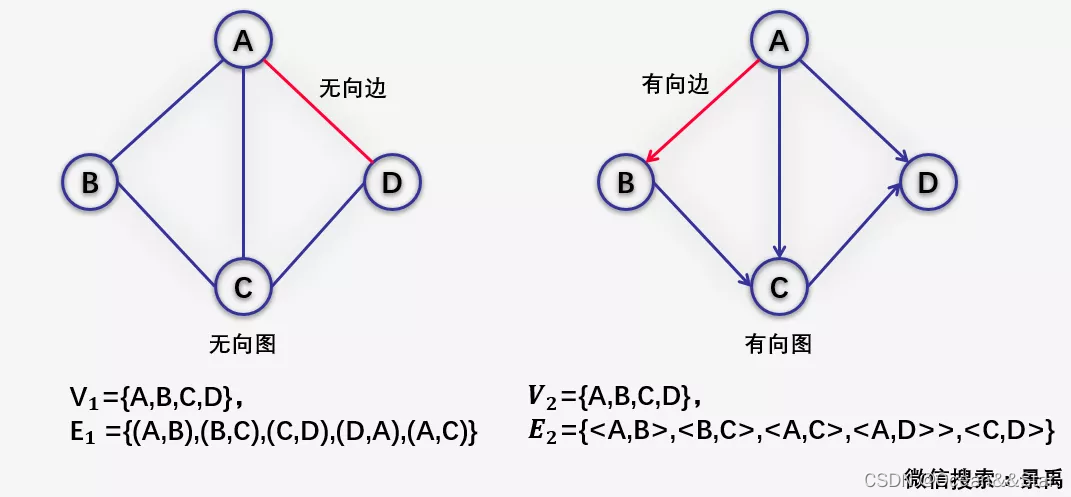
无向边 VS 有向边

• 无向边：
  • 顶点Vi与Vj之间的边没有方向，则称这条边为无向边(Edge)，用无序偶 (Vi，Vj) 来表示。
  • (Vi，Vj) 与 (Vj，Vi) 意义相同，表示x和y之间有连接。
• 有向边：
  • 若从顶点Vi与Vj之间的边有方向，则称这条边为有向边，也成为弧(Arc)，用有序偶<Vi，Vj>来表示，Vi为弧尾，Vj为弧头。
  • <Vi，Vj>与<Vj，Vi>表示的意义是不同的，<Vi，Vj>表示从Vi连接到Vj，Vi称为尾，Vj称为头；<Vj，Vi>表示从Vj连接到Vi，Vj称为尾，Vi称为头

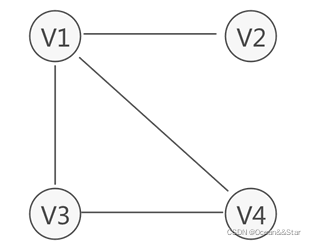
并且，图中习惯用 VR 表示图中所有顶点之间关系的集合。

下图无向图的集合 VR={(v1,v2),(v1,v4),(v1,v3),(v3,v4)}

下图有向图的集合VR={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}。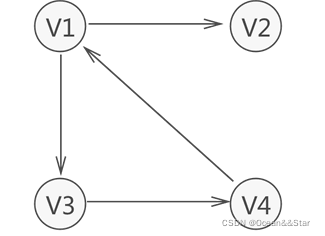

度、入度、出度

这是针对有向图的。

• 顶点 V 的度是和 V 相关联的边的数目，记为TD(V)
• 以顶点V为头的边的数目叫做入度（箭头指向 V的弧的数量），记为ID(V)
• 以顶点V为尾的边的数目叫做出度（箭头远离 V的弧的数量），记为 OD(V)
• 顶点的度 = 入度 + 出度。即 TD(V) = ID(V) + OD(V)。

下图中，$V_0$ 顶点的度为 3 ，入度为1，出度为2

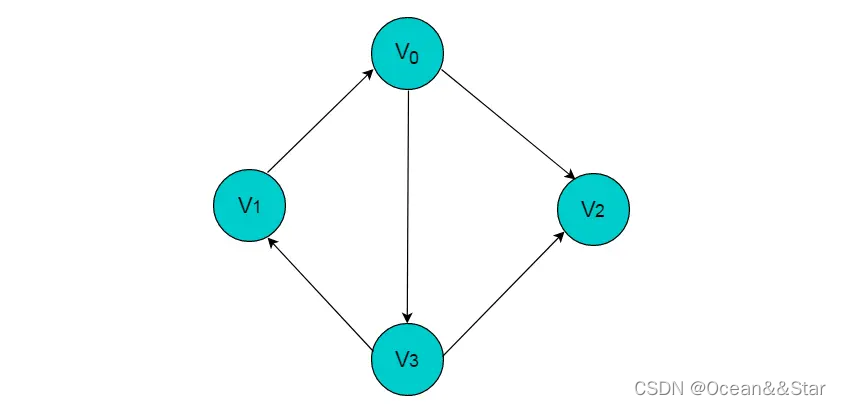
邻接

• 邻接是两个顶点之间的一种关系。如果图包含（u,v），则称顶点 v 与顶点 u 邻接。在无向图中，这也暗示了顶点 u 也与顶点 v 邻接。换句话说，在无向图中邻接关系是对称的。

各种图

简单图

在图结构中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。

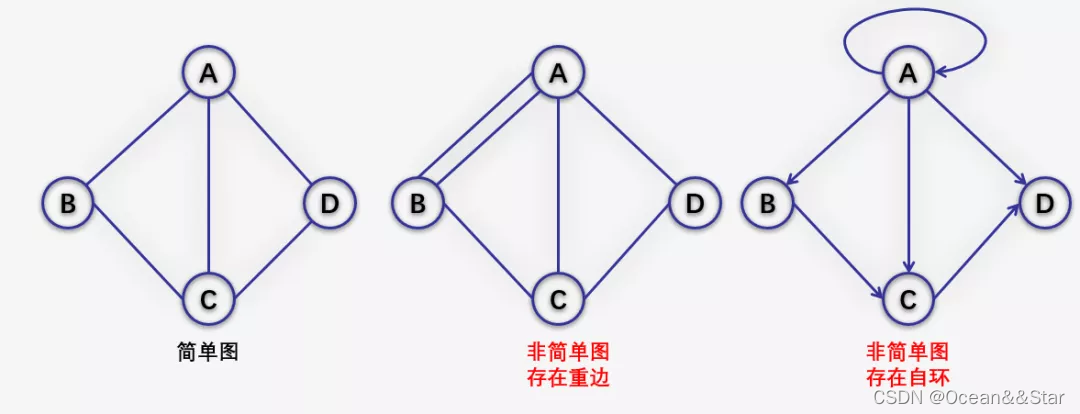
无向图 VS 有向图

• 无向图定义：若图中任意两个顶点之间的边均是无向边，则称该图为无向图
• 有向图定义：若图中任意两个顶点之间的边均是有向边，则称该图为有向图

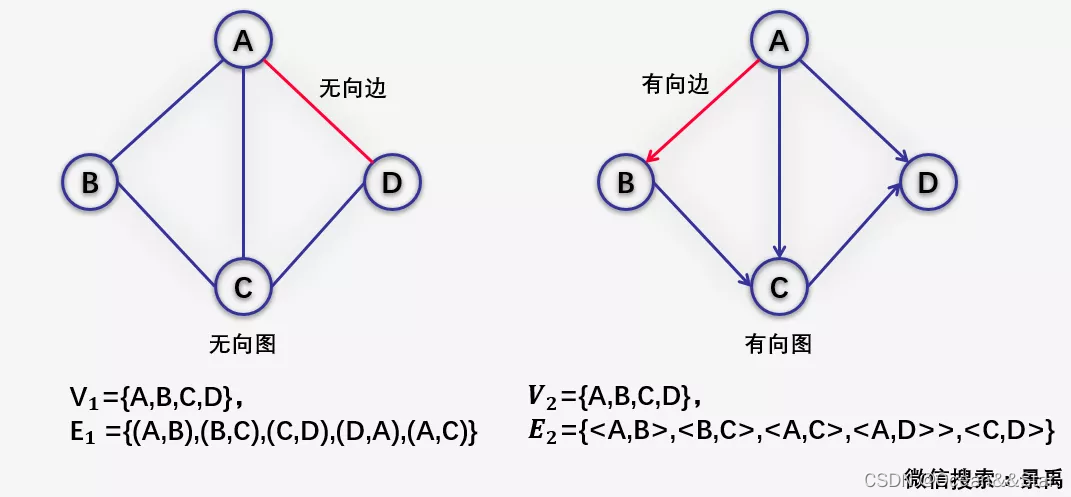
应用：

• 有向图中顶点之间的关联并不是完全对称的。还拿微信来举例，你的好友列表里有我，但我的好友列表里未必有你。这样一来，顶点之间的边就有了方向的区分，这种带有方向的图被称为有向图。
  
• 相应的，在QQ当中，只要我把你从好友里删除，你在自己的好友列表里也就看不到我了。因此，QQ的好友关系可以认为是一个没有方向区分的图，这种图被称为无向图。

完全图、无向完全图、有向完全图

• 完全图：若图中各个顶点都与除自身外的其他顶点有关系，这样的无向图称为完全图

• 无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图（含有n个顶点的无向完全图有(n×(n-1))/2条边

• 有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条边，则称该图为有向完全图。（含有 n 个顶点的有向完全图有 n×(n-1) 条边）

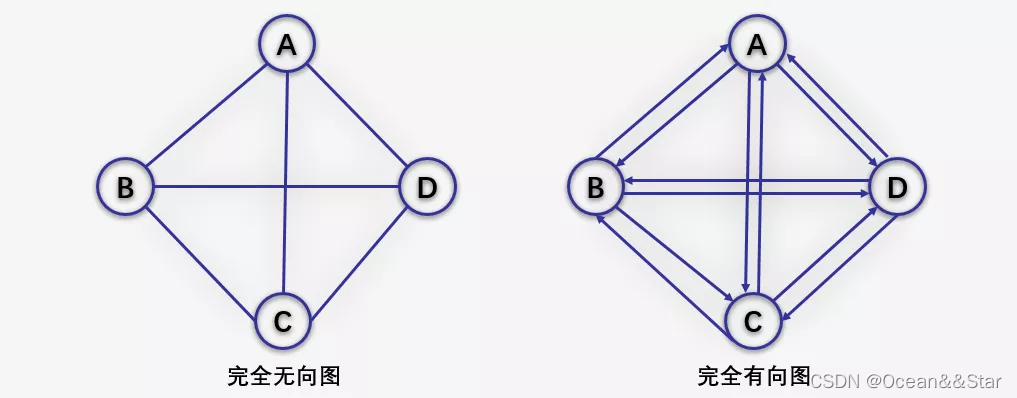
稀疏图 VS 稠密图

这里的稀疏和稠密是模糊的概念，都是相对而言的，通常认为边或弧数小于n*logn（n是顶点的个数）的图称为稀疏图，反之称为稠密图。

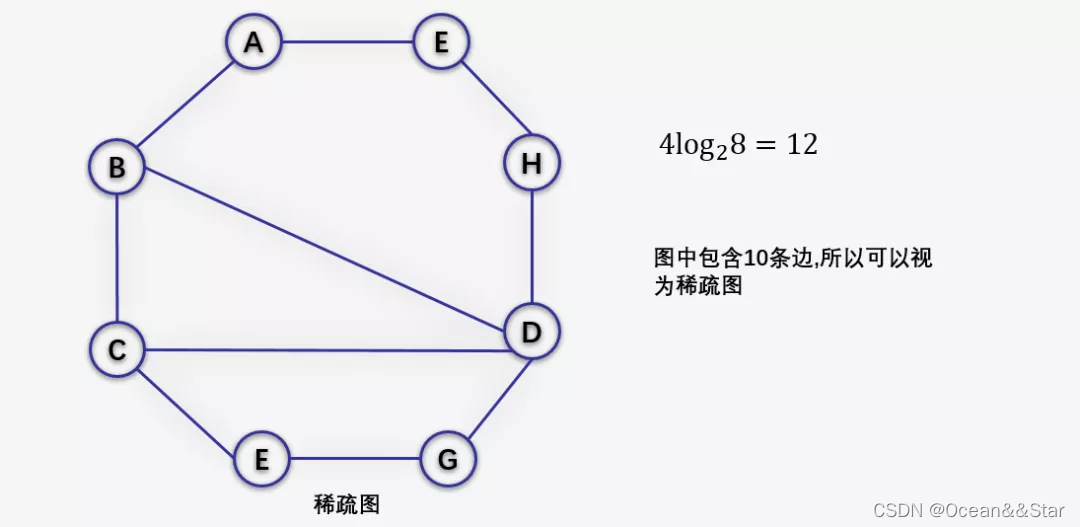
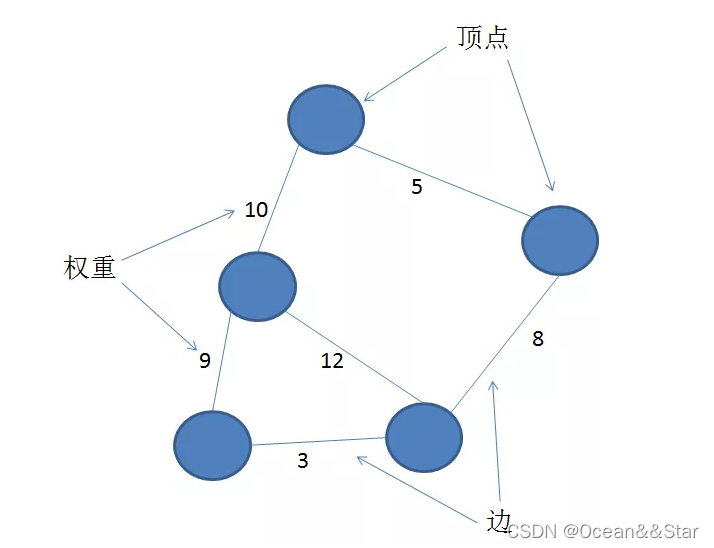
带权图

有些图的边或弧带有与它相关的数字，这种与图的边或弧相关的数叫做权(Weight)，带权的图通常称为网(Network)。

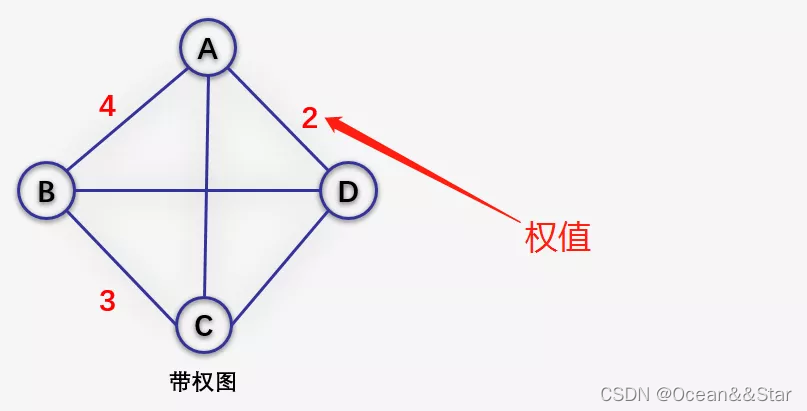
假设有两个图G1=(V1,E1)和G2=(V2,E2)，如果V2⊆V1，E2⊆E1，则称G2为G1的子图(Subgraph)。

连通图 VS 非连通图

在无向图G中，如果从顶点v到订单v’有路径，则称v和v’是连通的。如果对于图中任意两个顶点$vi、vj\in E$， vi，和vj都是连通的，则称 G 是连通图，否则图为非连通图。

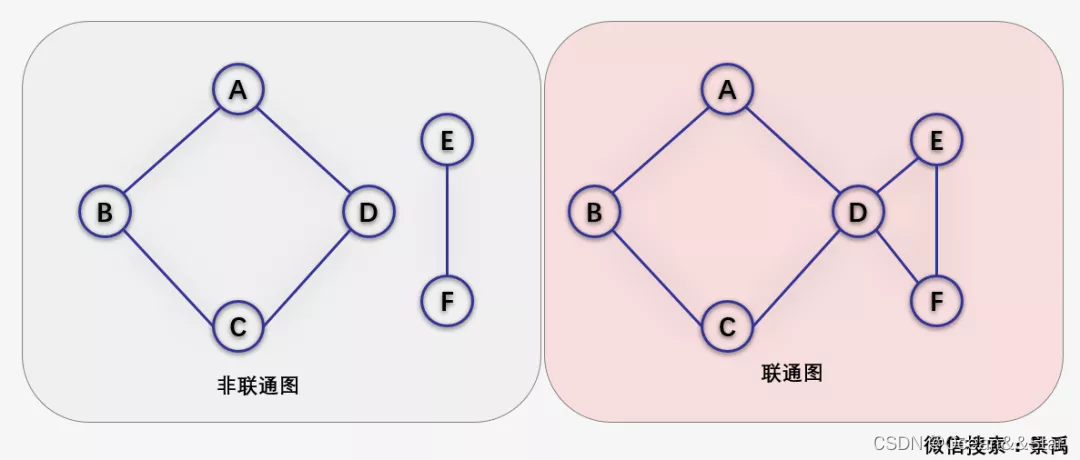
下图中A、B、C、D是连通的，但是其中任一顶点与顶点E或者顶点F之间没有路径，因此是非联通图

若添加顶点B与顶点F之间的邻接边，则图变为连通图

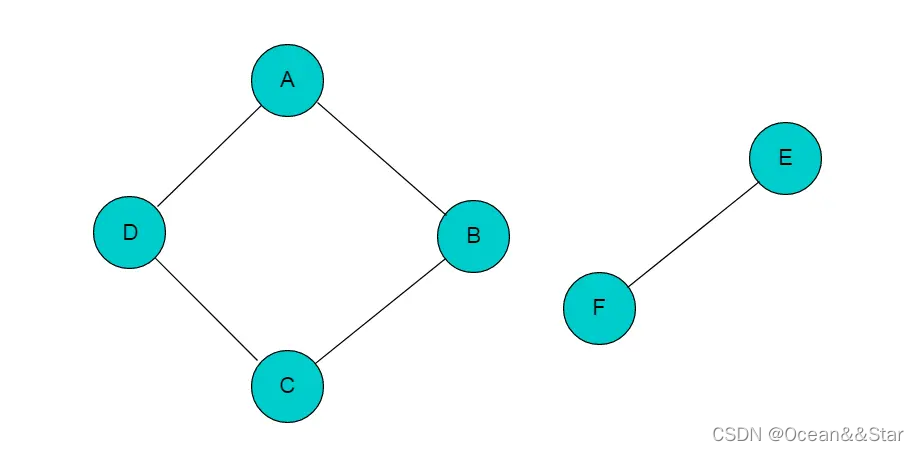
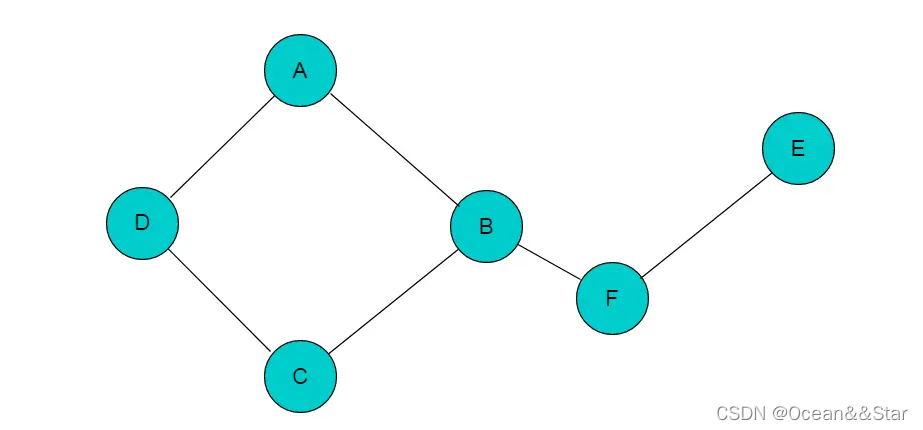
路径&&回路

• 路径：在图中，依次遍历顶点序列之间的边所形成的轨迹。

例如：下图中依次访问顶点 V0 、V3 和 V2 ，则构成一条路径。

如果路径中第一个顶点和最后一个顶点相同，则此路径称为"回路路"（或"环"）。

如下图，从 V1 存在一条路径还可以回到 V1，此路径为 {V1,V3,V4,V1}，这是一个回路（环），而且还是一个简单回路（简单环）

图的存储

邻接矩阵

• 图的数组存储方式也称为邻接矩阵存储。图中的数据信息包括：顶点信息和描述顶点之间关系的边的信息，将这两种信息存储在数组中就是图的数组存储。
• 首先，创建顶点数组，顶点数组中存储的是图的顶点信息，采用一维数组的方式即可存储所有的顶点信息。存储图中边的信息时，由于边是描述顶点与顶点之间关系的信息，因此需要采用二维数组进行存储。

定义：设图 G 有 n 个顶点，则邻接矩阵是一个$n\ast n$的方阵A，定义为：

其中， 或者(Vi , Vj,)表示顶点 Vi 与顶点 Vj 邻接。wi,j表示边的权重值。

无向图采用数组存储方式存储

例如：下图所示的无向图，采用数组存储形式如下。

注：图中的数组存储方式简化了边的权值为 1 。

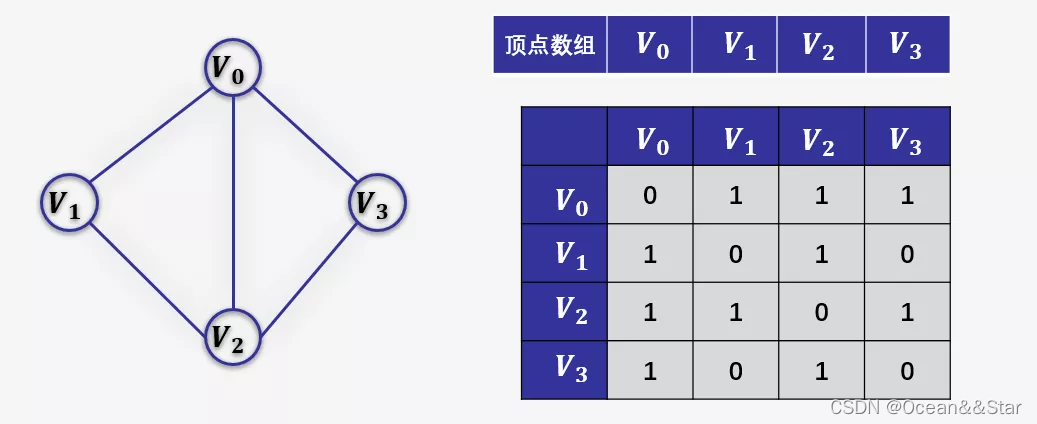
我们可以设置两个数组，顶点数组为$vertex[4]=V0,V1,V2,V3$，边数组$arc[4][4]$为对称矩阵(0表示不存在顶点间的边，1表示顶点间存在边)。

对称矩阵：所谓对称矩阵就是n阶矩阵的元素满足$a[i][j]=a[j][i](0<=i,j<=n)$。即从矩阵的左上角到右下角的主对角线为轴，右上角的元与左下角相对应的元全都是相等的。

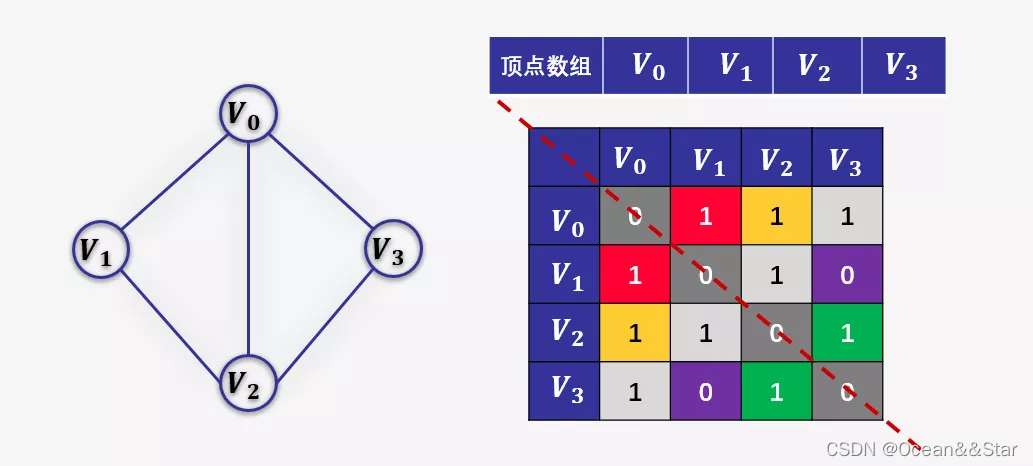
无向图的数组存储主要有以下特性：

• 顶点数组长度为0的顶点数目n。边数组为$n\ast n$的二维数组
• 边数组中，$A[i][j]=1$表示顶点i和顶点j邻接，$A[i][j]=0$代表顶点i与顶点j不邻接
• 在无向图中，由于边是无向边，因此顶点的邻接关系是对称的，边数组为对称二维数组
• 顶点与自身之间并未邻接关系（自己和自己不能邻接），因此边数组的对角线上的元素均为0
• 顶点的度即为顶点所在的行或者列1的数目。例如：顶点V2的度为3，则V2所在行和列中的1的数目为3。

有向图采用数组存储方式存储

无向图的边构成了一个对称矩阵，貌似浪费了一半的空间，那如果是有向图来存放，会不会把资源都利用得很好呢？

（1）普通有向图的邻接矩阵

可见顶点数组$vertex[4]=V0,V1,V2,V3$，弧数组$arc[4][4]$也是一个矩阵，但因为是有向图，所以这个矩阵并不对称，例如由V0到V3有弧，得到$arc[0][3]=1$，而V3到V0没有弧，因此$arc[3][0]=0$。

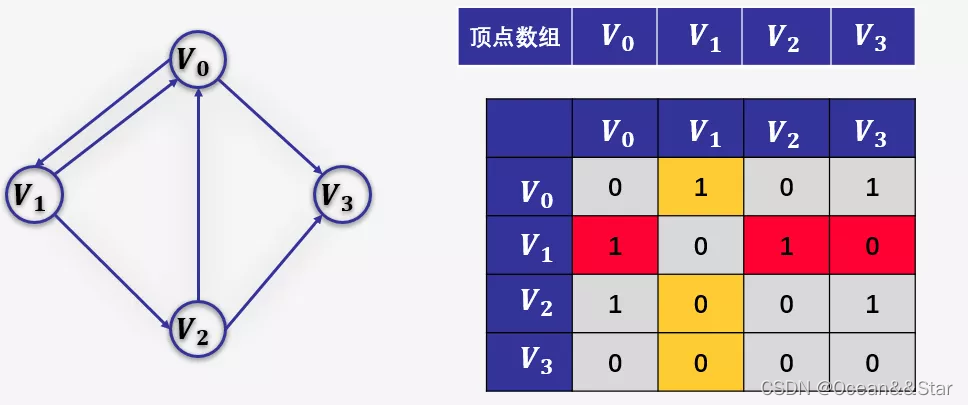
另外有向图是有讲究的，要考虑入度和出度，顶点V1的入度为1，正好是第V1列的各数之和，顶点V1的出度为2，正好是第V1行的各数之和。

（2）带权图的邻接矩阵

带权图中的每一条边上带有权值，邻接矩阵中的值则为权值，当两个顶点之间没有弧时，则用无穷大表示。

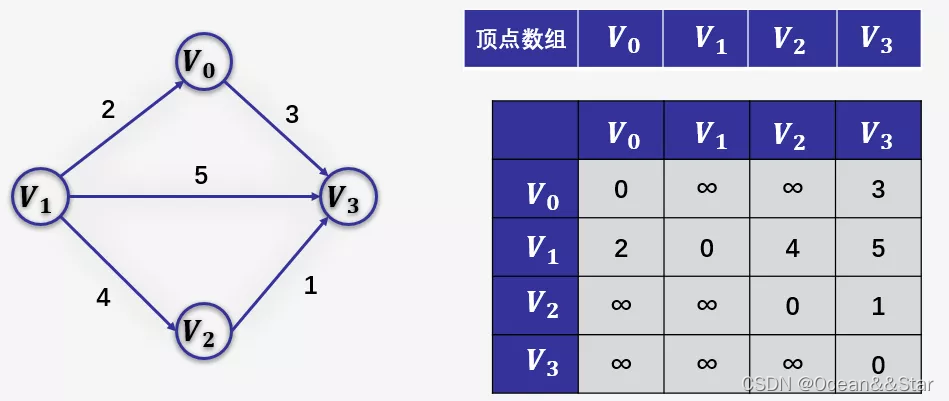
有向图的数组存储主要有以下特性：

• 顶点数组长度为0的顶点数目n。边数组为$n\ast n$的二维数组
• 边数组中，数组元素为1，即A[i][j] = 1,代表第i个顶点与第j个顶点邻接，且i为尾，j为头。 A[i][j] = 0代表顶点与顶点不邻接
• 在有向图中，由于边存在方向性，因此数组不一定为对称数组
• 对角线上元素为0
• 第i行中，1的数目代表第i个顶点的出度。例如：顶点V1的出度为2，则顶点V1所在行的1的数目为2。
• 第j列中，1的数目代表第j个顶点的入度。例如：V3的入度为1，则V3所在列中1的数目为1

数组存储方式优点：

• 数组存储方式容易实现图的操作。例如：求某顶点的度、判断顶点之间是否有边（弧）、找顶点的邻接点等等。

数组存储方式缺点：

• 采用数组存储方式，图若有n个顶点则需要n2个单元存储边(弧)，空间存储效率为O(n2)。 当顶点数目较多，边数目较少时，此时图为稀疏图，这时尤其浪费空间。
• 如下图，图中有 9 个顶点，边数为10，需要 9X9 的二维数组，而实际存储边信息空间只有10，造成空间浪费。
  

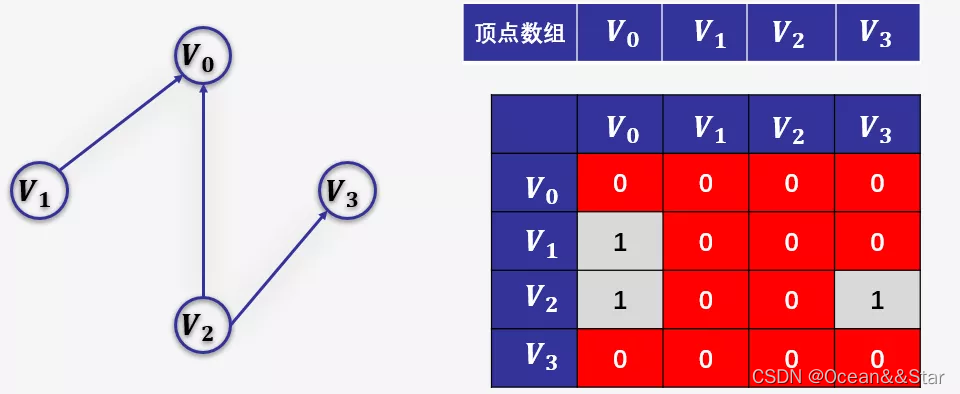
// 时间复杂度为O(n+n^2+e)#define MAXVEX 100 // 最大顶点数#define INFINITY 65535 // 用65535来代表无穷大typedef struct{
     char vexs[MAXVEX]; // 顶点表  int arc[MAXVEX][MAXVEX]; // 邻接矩阵  int numVertexes, numEdges; // 图中当前的顶点数和边数} MGraph;// 建立无向网图的邻接矩阵void CreateMGraph(MGraph *G){
     int i, j, k, w;    printf("请输入顶点数和边数：\n");  scanf("%d %d", &G->numVertexes, &G->numEdges);    for( i=0; i < G->numVertexes; i++ )  {
       scanf("%c", &G->vexs[i]);  }    for( i=0; i < G->numVertexes; i++ )  {
       for( j=0; j < G->numVertexes; j++ )    {
         G->arc[i][j] = INFINITY; // 邻接矩阵初始化    }  }    for( k=0; k < G->numEdges; k++ )  {
       printf("请输入边(Vi,Vj)上的下标i,下标j和对应的权w:\n"); // 这只是例子，提高用户体验需要进行改善    scanf("%d %d %d", &i, &j, &w);     G->arc[j][i] = G->arc[i][j] = w;   // 是无向网图，对称矩阵  }}

邻接表

当使用数组存储时，主要有以下三个问题

• 对于没一个图，如果图中顶点数目过大，则无法使用邻接矩阵进行存储。因此在分配数组内存时可能会导致内存分配失败
• 对于某些稀疏图（即顶点数目多，边数目少），创建的数组大小很大，而真正存储的有用信息又很少，这就造成了空间浪费
• 有时两个点之间不止存在一条边，这时用邻接矩阵就无法同时表示两条以上的边。

针对以上情况，提出了一种特殊的图存储方式，让每个节点拥有的数组大小刚好就等于它所连接的边数，由此建立一种邻接表的存储方式。

邻接表存储方法是一种数组存储和链式存储相结合的存储方法。

• 图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过数组可以较容易地读取顶点信息，更加方便。
• 图中每个顶点Vi的所有邻接点构成一个线性表，由于邻接点的个数不确定，所以我们选择用单链表来存储。

怎么定义呢：

• 在数组中存储叫做头节点，头结点由两个域组成，分别指向链表中第一个顶点和存储Vi的名或其他信息。具体结构如下图， 其中，data域中存储顶点相关信息，firstarc指向链表的第一个节点。：

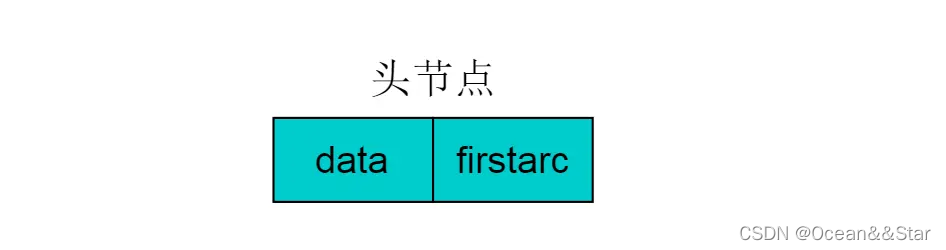
• 链表中的节点称为表节点，共有三个域，具体结构见下图，其中adjvex存储与Vi邻接的点在图中的位置，nextarc存储下一条边或弧的结点，data存储与边或弧相关的信息如权值.。

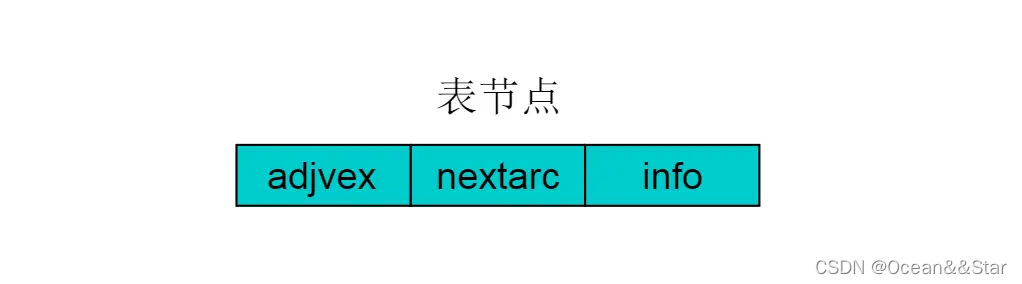
例子：

（1）无向图邻接表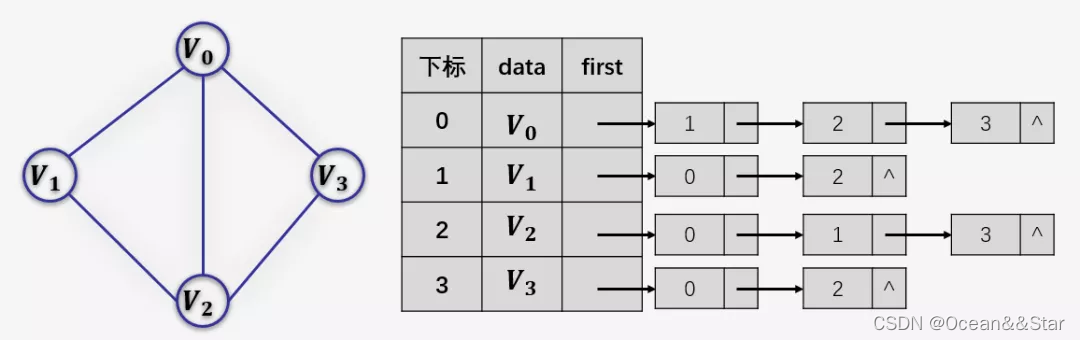

• 以V0顶点为例，V0顶点的邻接顶点为V1、V2、V3，则可以创建3个表节点，表节点中adjvex分别存储V1、V2、V3的索引1、2、3

无向图的邻接表存储特性：

• 数组中头节点的数目为图的顶点数目。
• 链表的长度就是顶点的度。比如，V0顶点的度为3，则以V0为头节点的链表中表节点的数目为3

（2）有向图邻接表：

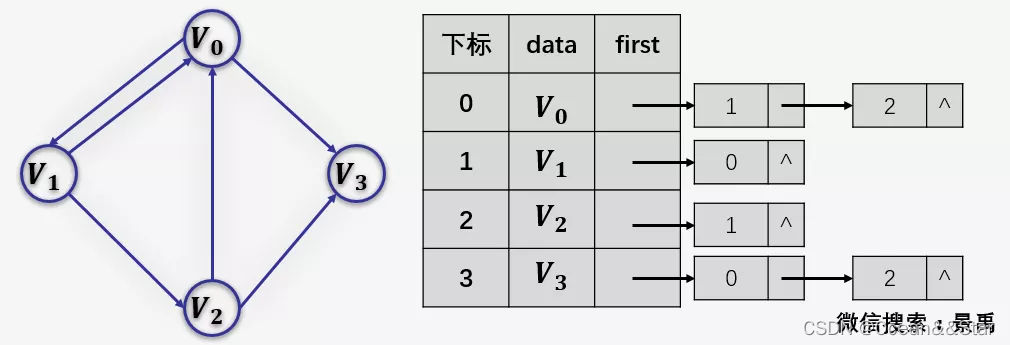
• 若是有向图，邻接表结构也是类似的，我们先来看下把顶点当弧尾建立的邻接表，这样很容易就可以得到每个顶点的出度（链表的长度即为顶点的出度，比如v0的出度就是2，V0为头节点的链表中，表节点的数目为2），但是想要得到顶点的入度，则需要遍历整个邻接表：

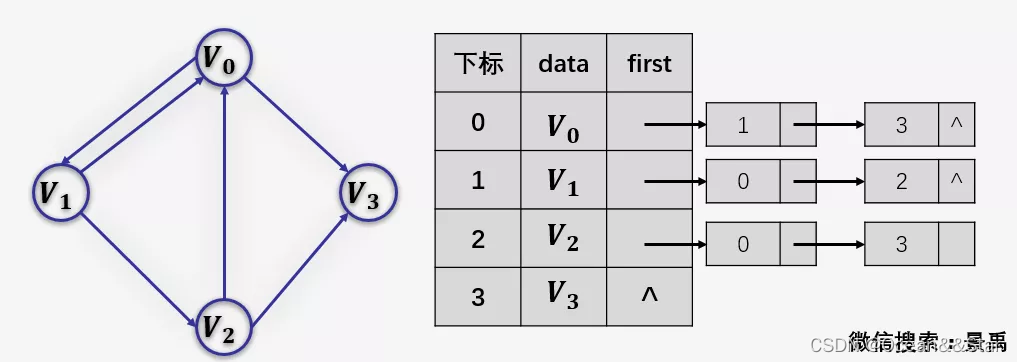
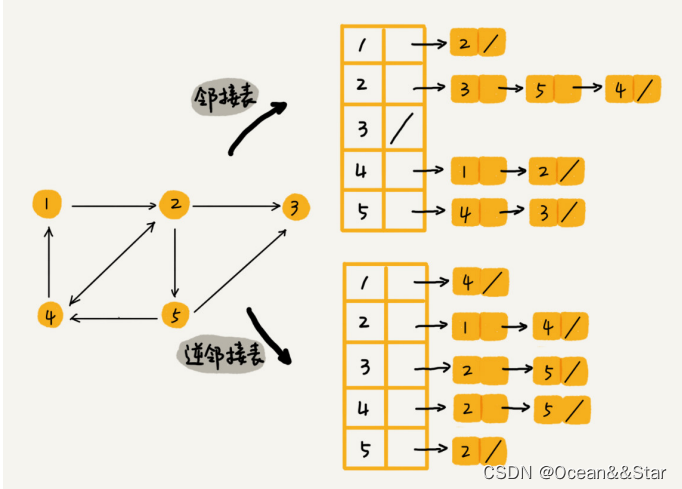
• 为了便于确定顶点的入度或以顶点为弧头的弧，我们可以建立一个有向图的逆邻接表：
  

（3）带权网络的邻接表

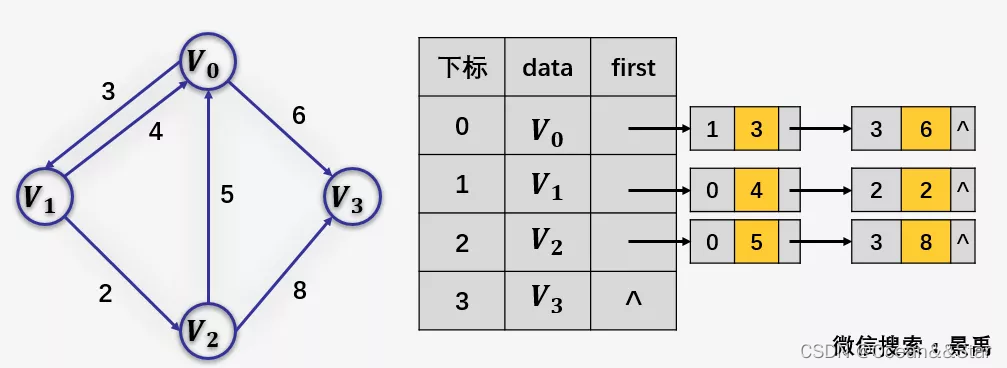
注：图采用邻接表的方式表示时，其表示方法是不唯一的。这是因为在每个顶点对应的单链表中，各边节点的链接次序是可以任意的，取决于建立邻接表的算法以及边的输入次序。

#define MAXVEX 100typedef struct EdgeNode      // 边表结点{
     int adjvex; // 邻接点域，存储该顶点对应的下标  int weight; // 用于存储权值，对于非网图可以不需要  struct EdgeNode *next;    // 链域，指向下一个邻接点} EdgeNode;typedef struct VertexNode    // 顶点表结点{
     char data; // 顶点域，存储顶点信息  EdgeNode *firstEdge; // 边表头指针} VertexNode, AdjList[MAXVEX];typedef struct{
     AdjList adjList;  int numVertexes, numEdges; // 图中当前顶点数和边数} GraphAdjList;// 建立图的邻接表结构void CreateALGraph(GraphAdjList *G){
     int i, j, k;  EdgeNode *e;    printf("请输入顶点数和边数：\n");  scanf("%d %d", &G->numVertexes, &G->numEdges);    // 读取顶点信息，建立顶点表  for( i=0; i < G->numVertexes; i++ )  {
       scanf("%c", &G->adjList[i].data);    G->adjList[i].firstEdge = NULL; // 初始化置为空表  }    for( k=0; k < G->numEdges; k++ )  {
       printf("请输入边(Vi,Vj)上的顶点序号：\n");    scanf("%d %d", &i, &j);        e = (EdgeNode *)malloc(sizeof(EdgeNode));    e->adjvex = j; // 邻接序号为j    e->next = G->adjList[i].firstEdge;    G->adjList[i].firstEdge = e;        e = (EdgeNode *)malloc(sizeof(EdgeNode));    e->adjvex = i; // 邻接序号为i    e->next = G->adjList[j].firstEdge;    G->adjList[j].firstEdge = e;  }}邻接表固然优秀，但也有不足，例如对有向图的处理上，有时候需要再建立一个逆邻接表~小禹

十字链表

对于有向图而言，邻接链表的缺陷是要查询某个顶点的入度时需要遍历整个链表，而逆邻接链表在查询某个顶点的出度时要遍历整个链表。

为了解决这些问题，十字链表将邻接链表和逆邻接链表综合了起来，而得到的一种十字链表。

在十字链表中，每一条边对应一种边节点，每一个顶点对应为顶点节点。

• 顶点节点即为头节点，由3个域构成，具体形式如下：

• 边节点为链表节点，共有 5个域（info省略了），具体形式如下：
  

为了更直观地理解十字链表，我们可以先看一下邻接表与逆邻接表的表示：

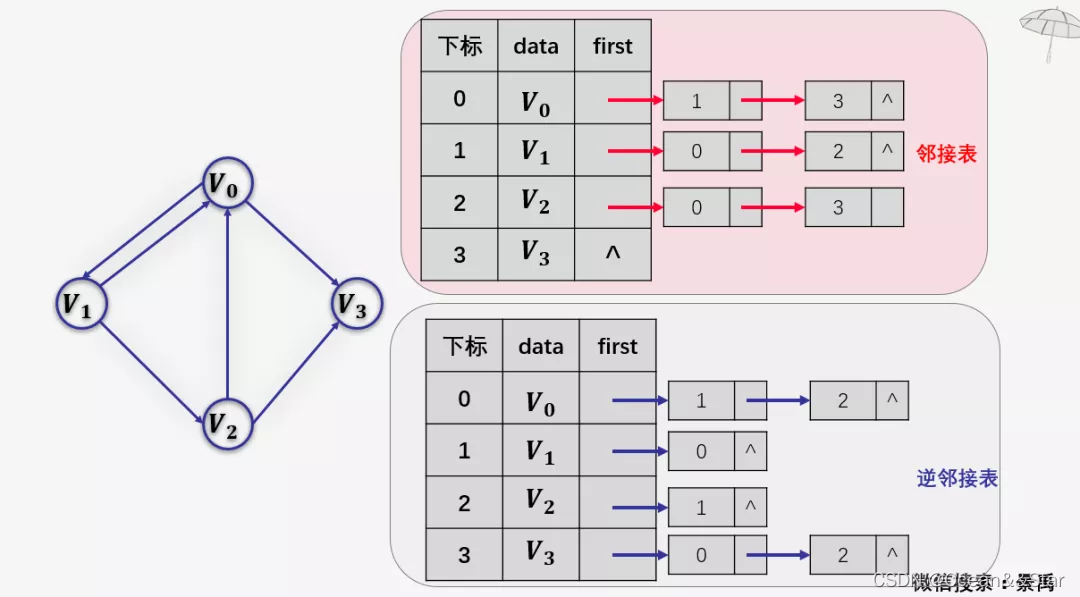十字链表的表示：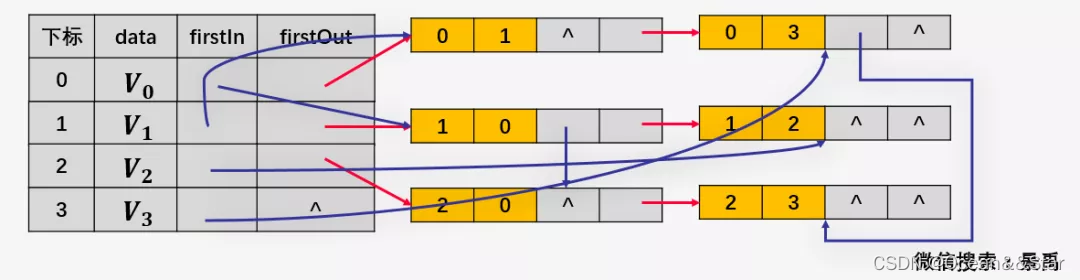

其中红色连接线与蓝色链接线分别代表邻接表表示与逆邻接表表示。

十字链表的好处就是因为把邻接表和逆邻接表整合在了一起，这样既容易找到以Vi为尾的弧，也容易找到以Vi为头的弧，因而容易求得顶点的出度和入度。

十字链表除了结构复杂一点外，其实创建图算法的时间复杂度是和邻接表相同的，因此，在有向图的应用中，十字链表也是非常好的数据结构模型。

邻接多重表

如果我们在无向图的应用中，关注的重点是顶点的话，那么邻接表是不错的选择，但如果我们更关注的是边的操作，比如对已经访问过的边做标记，或者删除某一条边等操作，邻接表的确显得不那么方便了（下图中删除红色边）。

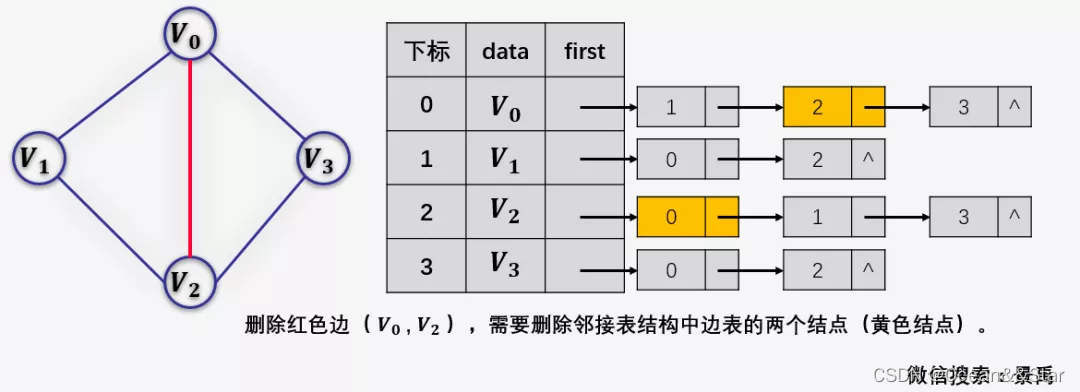
邻接表对边的操作显然很不方便，因此，我们可以仿照十字链表的方式，对边表结构进行改装

邻接多重表仿照了十字链表的思想，对邻接链表的边表结点进行了改进：对于无向图而言，其每条边在邻接链表中都需要两个结点来表示，而邻接多重表正是对其进行优化，让同一条边只用一个结点表示即可。

重新定义的边结点结构如下图：

其中，ivex和jvex是指某条边依附的两个顶点在顶点表中的下标。 ilink指向依附顶点ivex的下一条边，jlink指向依附顶点jvex的下一条边。info存储边的相关信息。

重新定义的顶点结构如下图：

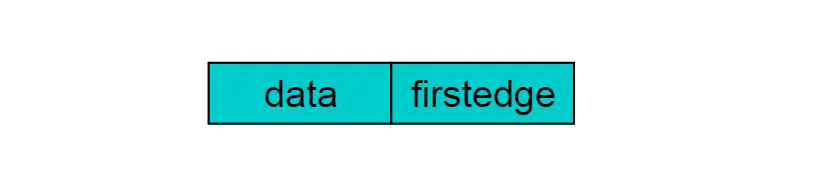
也就是说在邻接多重表里边，边表存放的是一条边，而不是一个顶点。

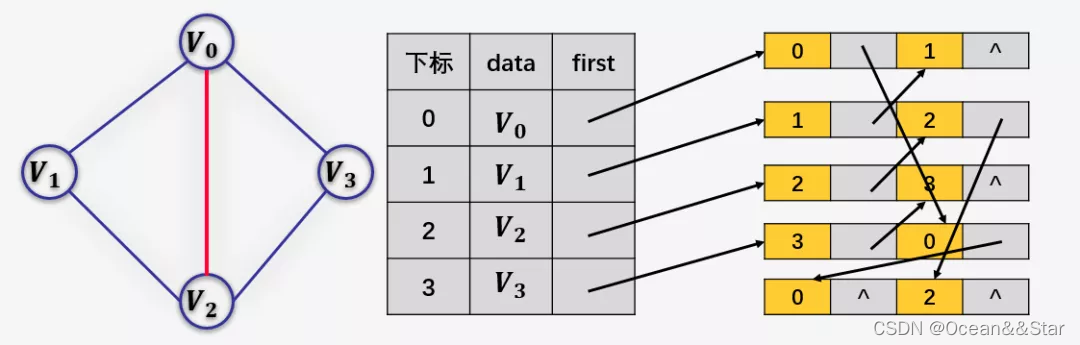
这样删除一条边就容易多了。

例子，采用邻接多重表存储下面无向图

以V0为例，顶点data域存储V0名称，firstedge指向(V0，V1)的边，边节点中的ilink指向依附V0顶点的下一条边(V0 , V3)，jlink指向依附V1顶点的下一条边(V1 , V2)，按照此方式建立邻接多重表：

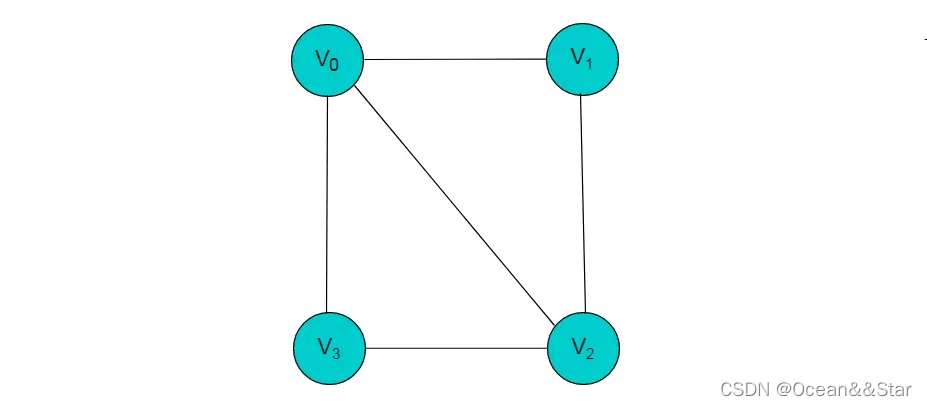
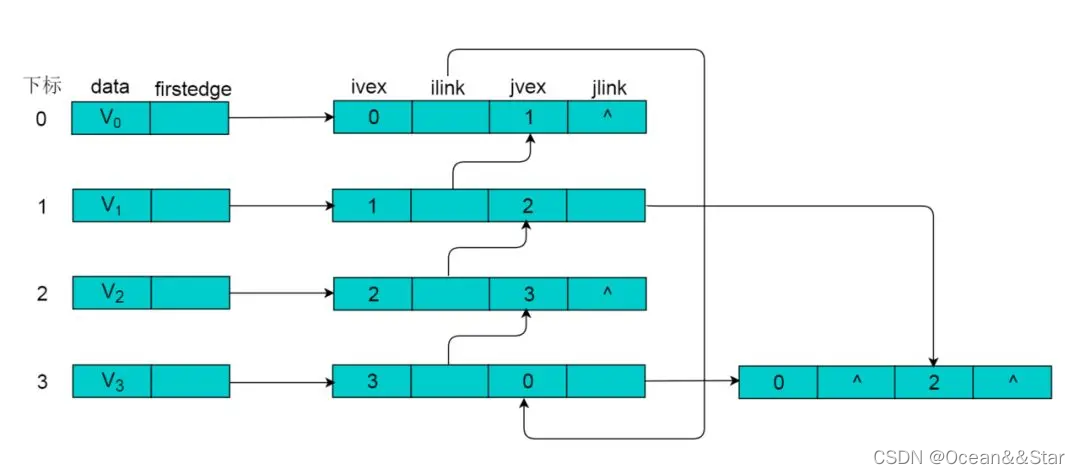
边集数组

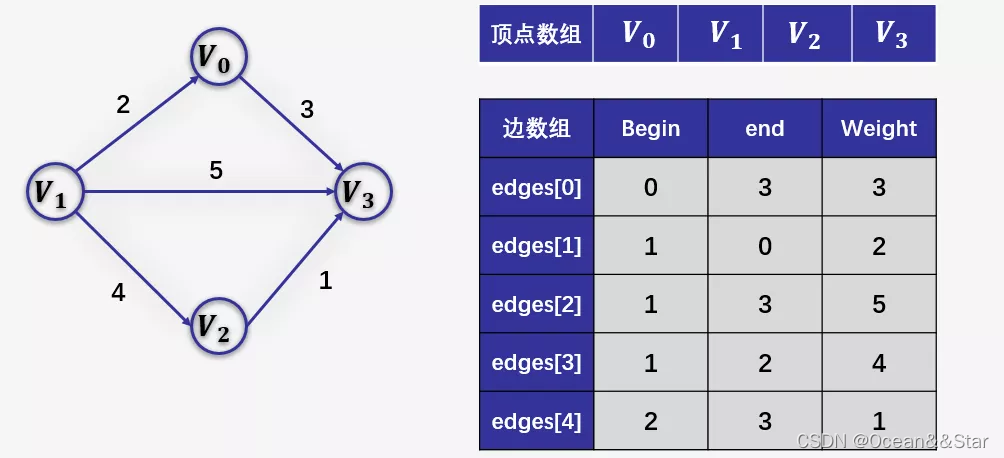
边集数组是由两个一维数组构成，一个是存储顶点的信息，另一个是存储边的信息，这个边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成。

转载地址：https://blog.csdn.net/zhizhengguan/article/details/122474058 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！