
本文共 2509 字,大约阅读时间需要 8 分钟。
学完线性回归,逻辑回归建模+评估模型的过程就相对好理解很多。其实就是换汤不换药。
逻辑回归不是回归算法,而是分类算法,准确来说,叫逻辑分类
逻辑分类本质上是二分分类,即分类结果标签只有两个
逻辑回归建模-评估模型的过程
如何建立有序的二维数据结构
1.字典是无序的,所以引入一个OrderedDict来让顺序变成有序
2.数据集转成Pandas的二维数据结构进行处理
如何实现逻辑回归
1.提取出特征和标签
提取出某一列:loc (根据索引进行提取)
2.建立训练数据和测试数据
从样本中随机的按比例选取训练数据(train)和测试数据(test):
使用交叉验证(sklearn.model_selection)中的train_test_split
train_test_split三个参数:
第一个参数:所要划分的样本特征
第二个参数:所要划分的标签特征
第三个参数:train_size= (<0的小数:训练数据的占比 >0的整数:样本的数量)
x_train , x_test , y_train , y_test 各分配到一定比例的数据
3.使用训练数据训练模型
注意:sklearn要求输入的特征必须是二维数组的类型,但是因为我们目前只有1个特征,所以需要用安装错误提示用reshape转行成二维数组的类型
导入逻辑回归:使用sklearn.linear_model中的LogisticRegression
用LogisticRegression创建训练模型:model = LogisticRegression()
训练模型:用的是fit函数
model.fit(x_train , y_train)
4.使用测试数据进行模型评估
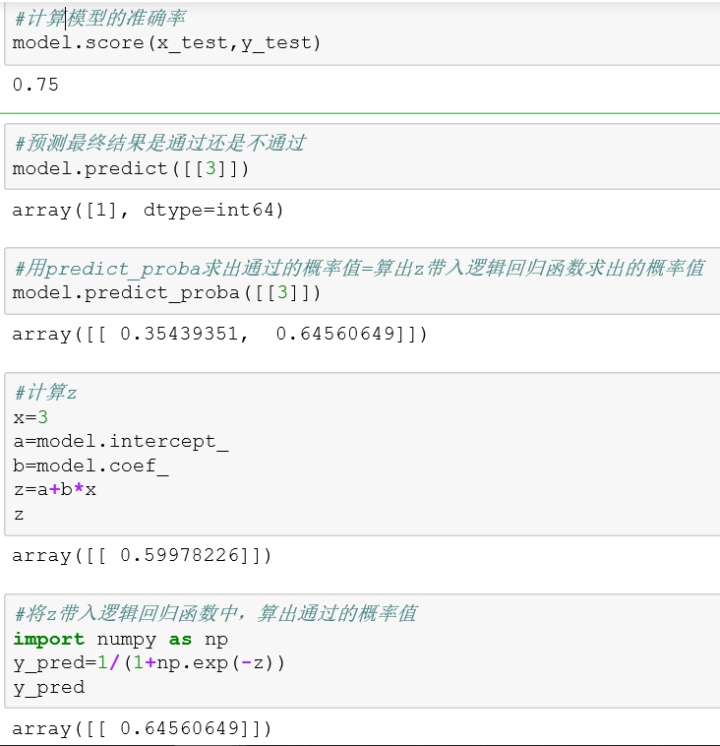
评估模型准确度 准确率 :score函数
model.score(x_test,y_test)
5.进一步理解什么是逻辑函数
预测数据的结果用predict: model.predict([[3]])
得出的结果要么0要么1
1)用predict_probe获取概率值
model.predict_proba([[3]])
输出结果第1个值是标签为0的概率值,第2个值是标签为1的概率值
2)用逻辑回归函数获取概率值
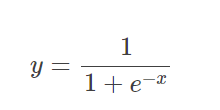
逻辑回归函数 第一步要得到z值
z=a+bx
a:截距 a=model.intercept_
b:回归系数 b=model.coef_
将z值带入逻辑回归函数中,得到概率值
y_pred=1/(1+np.exp(-z))
e:通过Numpy中的exp函数求得
逻辑回归代码
#建立有序的二维数据结构import pandas as pdfrom collections import OrderedDictexamDict={ '学习时间':[0.50,0.75,1.00,1.25,1.50,1.75,1.75,2.00,2.25,2.50, 2.75,3.00,3.25,3.50,4.00,4.25,4.50,4.75,5.00,5.50], '通过考试':[0,0,0,0,0,0,1,0,1,0,1,0,1,0,1,1,1,1,1,1]}examOrder=OrderedDict(examDict)examDf=pd.DataFrame(examOrder)examDf.head() #1.提取出特征和标签x_exam=examDf.loc[:,'学习时间']y_exam=examDf.loc[:,'通过考试'] #2.建立训练数据和测试数据from sklearn.model_selection import train_test_splitx_train, x_test, y_train, y_test=train_test_split(x_exam, y_exam, train_size=0.8)print(x_exam.shape)print(y_exam.shape)print(x_train.shape)print(x_test.shape)print(y_train.shape)print(y_test.shape) #绘制测试数据和训练数据的散点图import matplotlib.pyplot as pltplt.scatter(x_train, y_train, color="blue", label="train data")plt.scatter(x_test, y_test, color="red", label="test data")plt.legend(loc=2)plt.xlabel("Hours")plt.ylabel("Pass")plt.show() #3.使用训练数据训练模型x_train=x_train.reshape(-1,1)y_train=y_train.reshape(-1,1) from sklearn.linear_model import LogisticRegressionmodel=LogisticRegression()model.fit(x_train, y_train) #4.使用测试数据进行模型评估x_test=x_test.reshape(-1,1)y_test=y_test.reshape(-1,1)model.score(x_test,y_test) #5.计算模型的准确率model.score(x_test,y_test) #预测最终结果是通过还是不通过model.predict([[3]]) #用predict_proba求出通过的概率值=算出z带入逻辑回归函数求出的概率值#计算概率值得方法1model.predict_proba([[3]])#计算概率值得方法2x=3a=model.intercept_b=model.coef_z=a+b*x#将z带入逻辑回归函数中,算出通过的概率值import numpy as npy_pred=1/(1+np.exp(-z))y_pred 转载地址:https://blog.csdn.net/weixin_39626369/article/details/110972893 如侵犯您的版权,请留言回复原文章的地址,我们会给您删除此文章,给您带来不便请您谅解!
发表评论
最新留言
关于作者
