本文共 12363 字，大约阅读时间需要 41 分钟。

算法导论

第一章 算法概论

描述方法：自然语言、流程图、程序设计语言、伪代码

算法设计要求：正确性、可读性、健壮性、高效性 时间复杂度排序： $$O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)$$ O() 指时间复杂度上界

第二章 递归与分治

递归算法优劣

优点：正确性易证明，适合分析、设计。

缺点：执行效率不高，堆栈空间浪费。

分治法

分而治之，将问题分解、求解、合并

分治时间复杂度计算方法

主方法

$$T(n)=aT(\frac{n}{b})+f(n)$$

将时间为 $n$ 的问题分解为 $a$ 个子问题，每个子问题的大小为 $\frac{n}{b}$ 设 $a>=1$，$b>1$ 为常数，$f(n)$ 为一个函数，则 $T(n)$ 计算如下：

1. 若对某些常数 $\epsilon >0$，有 $f(n)=O(n^{lo{g}_{b}a-\epsilon })$，$T(n)=O(n^{lo{g}_{b}a})$。
2. 若 $f(n)=O(n^{lo{g}_{b}a})$，$T(n)=O(n^{lo{g}_{b}a})lo{g}_{2}n$。
3. 对于某些常数 $\epsilon >0$，$f(n)=O(n^{lo{g}_{b}a+\epsilon })$，并且对常数 $c<1$ 与所有足够大的 $n$ 有 $af(\frac{n}{b})<=cf(n)$，$T(n)=O(f(n))$。

存在三种情况：

1. 函数 $n^{lo{g}_{b}a}$ 比函数 $f(n)$ 更大，则 $T(n)=O(n^{lo{g}_{b}a})$。
2. 函数 $n^{lo{g}_{b}a}$ 跟函数 $f(n)$ 一样大，则 $T(n)=O(n^{lo{g}_{b}a})lo{g}_{2}n$。
3. 函数 $n^{lo{g}_{b}a}$ 比函数 $f(n)$ 小，则 $T(n)=O(f(n))$。

二分搜索

时间复杂度 $O(logn)$

int binary_search(int a[], int x, int n) {
       int l, mid, r;    l = 0;    r = n - 1;    while (l < r) {
           mid = (l + r) / 2;        if (a[mid] == x) {
               return mid;        } else if (a[mid] > x) {
               r = mid - 1;        } else {
               l = mid + 1;        }    }    return -1;}

大整数乘法

说实话，在算法比赛中基本不用的东西。

$$XY=AB{2}^n+((A-B)(D-C)+AC+BD)2^{\frac{n}{2}}+BD$$ $$T(n)=\{\begin{array}{rlr}O(1)& & n=1\\ 3T(\frac{n}{2})+O(n)& & n>1\end{array}$$ $$T(n)=O(n^{log3})=O(n^{1.59})$$

棋盘覆盖问题（分治）

一个2^k * 2^k个方格组成的棋盘中，若恰有一个方格与其它方格不同，则称该方格为一特殊方格，称改棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有4^k种情形。因而对任何k>=0，有4^k种不同的特殊棋盘。下图所示的特殊棋盘为k=2时16个特殊棋盘中的一个。

在棋盘覆盖问题中，要用下图中4中不同形态的L型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。易知，在任何一个2^k * 2^k的棋盘中，用到的L型骨牌个数恰为(4^k-1)/3。

用分治策略，可以设计解棋盘问题的一个简捷的算法。

当k>0时，将 2^k *2^k 棋盘分割为4个 2^(k-1) * 2^(k-1) 子棋盘，如下图所示。

特殊方格必位于4个较小子棋盘之一中，其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘，我们可以用一个L型骨牌覆盖这3个较小的棋盘的汇合处，如下图所示，这3个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将原问题化为4个较小规模的棋盘覆盖问题。递归的使用这种分割，直至棋盘简化为1x1棋盘。

代码实现（跟书上的有出入）

#include 
   
    using namespace std;int tile = 1;         //L型骨牌的编号(递增)int Board[100][100];  //棋盘/*** 递归方式实现棋盘覆盖算法* 输入参数：* tr--当前棋盘左上角的行号* tc--当前棋盘左上角的列号* dr--当前特殊方格所在的行号* dc--当前特殊方格所在的列号* size：当前棋盘的:2^k**/void ChessBoard(int tr, int tc, int dr, int dc, int size) {
       if (size == 1) return;    int t = tile++, s = size / 2;    // 在左上角区域内    if (dr < tr + s && dc < tc + s) {
           ChessBoard(tr, tc, dr, dc, s);    } else {
           // 不在左上角区域内        // t：L型骨牌覆盖右下角        Board[tr + s - 1][tc + s - 1] = t;        // 覆盖剩余方格        ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);    }    // 在右上角区域内    if (dr < tr + s && dc >= tc + s) {
           ChessBoard(tr, tc + s, dr, dc, s);    } else {
           // 不在右上角的区域内        Board[tr + s - 1][tc + s] = t;        ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);    }    if (dr >= tr + s && dc < tc + s) {
           ChessBoard(tr + s, tc, dr, dc, s);    } else {
           Board[tr + s][tc + s - 1] = t;        ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);    }    if (dr >= tr + s && dc >= tc + s) {
           ChessBoard(tr + s, tc + s, dr, dc, s);    } else {
           Board[tr + s][tc + s] = t;        ChessBoard(tr + s, tc + s, tr + s, tc + s, s);    }}int main() {
       int size;    cout << "输入棋盘的size(大小必须是2的n次幂): ";    cin >> size;    int index_x, index_y;    cout << "输入特殊方格位置的坐标: ";    cin >> index_x >> index_y;    ChessBoard(0, 0, index_x - 1, index_y - 1, size);    for (int i = 0; i < size; i++) {
           for (int j = 0; j < size; j++) {
               cout << Board[i][j] << '\t';        }        cout << endl;    }}
   

线性时间选择（分治）

给定线性序集中n个元素和一个整数k，1≤k≤n，要求找出这n个元素中第k小的元素。

解决方法

1. 将n个输入元素划分成n/5（向上取整）个组，每组5个元素，最多只可能有一个组不是5个元素。用任意一种排序算法，将每组中的元素排好序，并取出每组的中位数，共n/5（向上取整）个。
2. 递归调用select来找出这n/5（向上取整）个元素的中位数。如果n/5（向上取整）是偶数，就找它的2个中位数中较大的一个。以这个元素作为划分基准。

代码实现

#include 
   
    using namespace std;void bubbleSort(int a[], int p, int r) {
       for (int i = p; i < r; i++) {
           for (int j = i + 1; j <= r; j++) {
               if (a[j] < a[i]) {
                   swap(a[i], a[j]);            }        }    }}int Partition(int a[], int p, int r, int val) {
       int pos;    for (int q = p; q <= r; q++) {
           if (a[q] == val) {
               pos = q;            break;        }    }    swap(a[p], a[pos]);    int i = p, j = r + 1, x = a[p];    while (1) {
           while (a[++i] < x && i < r);        while (a[--j] > x);        if (i >= j)break;        swap(a[i], a[j]);    }    a[p] = a[j];    a[j] = x;    return j;}int Select(int a[], int p, int r, int k) {
       if (r - p < 75) {
           bubbleSort(a, p, r);        return a[p + k - 1];    }    //找中位数的中位数，r-p-4即上面所说的n-5    for (int i = 0; i <= (r - p - 4) / 5; i++) //把每个组的中位数交换到区间[p,p+(r-p-4)/4]    {
           int s = p + 5 * i, t = s + 4;        for (int j = 0; j < 3; j++) //冒泡排序，从后开始排，结果使得后三个数是排好顺序的（递增）        {
               for (int n = s; n < t - j; n++) {
                   if (a[n] > a[n + 1]) {
                       swap(a[n], a[n - 1]);                }            }        }        swap(a[p + i], a[s + 2]);//交换每组中的中位数到前面    }    //(r-p-4)/5表示组数-1，则[p,p+(r-p-4)/5]的区间长度等于组数    int x = Select(a, p, p + (r - p - 4) / 5, (r - p + 1) / 10);//求中位数的中位数    // (r-p+1)/10 = (p+(r+p-4)/5-p+1)/2=    int i = Partition(a, p, r, x), j = i - p + 1;    if (k <= j) {
           return Select(a, p, i, k);    } else {
           return Select(a, i + 1, r, k - j);    }}int main() {
       int x;    //数组a存了0-79，也可自行输入    int a[80] = {
   3, 1, 7, 6, 5, 9, 8, 2, 0, 4, 13, 11, 17, 16, 15, 19, 18, 12, 10, 14, 23, 21, 27, 26, 25, 29, 28, 22,                 20, 24, 33, 31, 37, 36, 35, 39, 38, 32, 30, 34, 43, 41, 47, 46, 45, 49, 48, 42, 40, 44, 53, 51, 57, 56,                 55, 59, 58, 52, 50, 54, 63, 61, 67, 66, 65, 69, 68, 62, 60, 64, 73, 71, 77, 76, 75, 79, 78, 72, 70, 74,    };    cin >> x;    printf("第%d大的数是%d\n", x, Select(a, 0, 79, x));}
   

归并排序（分治）

很简单，没什么可说的。

最接近点问题

一维太简单不写了（O(N)的复杂度足够）

二维最接近点问题

n个点在公共空间中，求出所有点对的欧几里得距离最小的点对。

1. 分解
   对所有的点按照x坐标（或者y）从小到大排序（排序方法时间复杂度O(nlogn)）。
   根据下标进行分割，使得点集分为两个集合。
2. 解决
   递归的寻找两个集合中的最近点对。
   取两个集合最近点对中的最小值 $min(di{s}_{left}，di{s}_{right}$)。
3. 合并
   最近距离不一定存在于两个集合中，可能一个点在集合A，一个点在集合B，而这两点间距离小于dis。
   根据递归的方法可以计算出划分的两个子集中所有点对的最小距离$di{s}_{left}$， $di{s}_{right}$，再比较两者取最小值，即 $dis=min(di{s}_{left}，di{s}_{right})$。那么一个点在集合A，一个在集合B中的情况，可以针对此情况，用之前分解的标准值，即按照x坐标（或者y）从小到大排序后的中间点的x坐标作为mid，划分一个$[mid-dis,mid+dis]$区域，如果存在最小距离点对，必定存在这个区域中。
   
   之后只需要根据$[mid-dis,mid]$左边区域的点来遍历右边区域$[mis,mid+dis]$的点，即可找到是否存在小于dis距离的点对。

时间复杂度

在分解和合并时，可能存在按照x轴、y轴进行排序的预处理O(nlogn)，该问题在解决阶段只做提取的操作为O(n)，递推式为：

$$T(n)=\{\begin{array}{rlr}1& & n<=3\\ 2T(\frac{n}{2})+O(n)& & n>3\end{array}$$

代码实现

#include 
   
    using namespace std;struct point {
       double x;    double y;    point(double x, double y) : x(x), y(y) {
   }    point() {
    return; }};// 比较x坐标bool cmp_x(const point &A, const point &B) {
       return A.x < B.x;}// 比较y坐标bool cmp_y(const point &A, const point &B) {
       return A.y < B.y;}double distance(const point &A, const point &B) {
       return sqrt(pow(A.x - B.x, 2) + pow(A.y - B.y, 2));}/** * 合并，同第三区域最近点距离比较 * @param points 点的集合 * @param dis 左右两边集合的最近点距离 * @param mid x坐标排序后，点集合中中间点的索引值 * @return  */double merge(vector
    
      &points, double dis, int mid) {
       vector
     
       left, right;    for (int i = 0; i < points.size(); ++i)  // 搜集左右两边符合条件的点    {
           if (points[i].x - points[mid].x <= 0 && points[i].x - points[mid].x > -dis) {
               left.push_back(points[i]);        } else if (points[i].x - points[mid].x > 0 && points[i].x - points[mid].x < dis) {
               right.push_back(points[i]);        }    }    sort(right.begin(), right.end(), cmp_y);    for (int i = 0, index; i < left.size(); ++i)  // 遍历左边的点集合，与右边符合条件的计算距离    {
           for (index = 0; index < right.size() && left[i].y < right[index].y; ++index);        for (int j = 0; j < 7 && index + j < right.size(); ++j)  // 遍历右边坐标上界的6个点        {
               if (distance(left[i], right[j + index]) < dis) {
                   dis = distance(left[i], right[j + index]);            }        }    }    return dis;}double closest(vector
      
        &points) {
       if (points.size() == 2) {
           return distance(points[0], points[1]);    }    if (points.size() == 3) {
           return min(distance(points[0], points[1]),                   min(distance(points[0], points[2]), distance(points[1], points[2])));    }    int mid = (points.size() >> 1) - 1;    double d1, d2, d;    vector
       
         left(mid + 1), right(points.size() - mid - 1);    // 左边区域点集合    copy(points.begin(), points.begin() + mid + 1, left.begin());    // 右边区域点集合    copy(points.begin() + mid + 1, points.end(), right.begin());    d1 = closest(left);    d2 = closest(right);    d = min(d1, d2);    return merge(points, d, mid);}int main() {
       int count;    printf("点个数：");    scanf("%d", &count);    vector
        
          points; double x, y; for (int i = 0; i < count; ++i) { printf("第%d个点", i); scanf("%lf%lf", &x, &y); point p(x, y); points.push_back(p); } sort(points.begin(), points.end(), cmp_x); printf("最近点对值：%lf", closest(points)); return 0;}
        
       
      
     
    
   

循环赛日程表

代码（最优日程）

#include
   
    using namespace std;#define ll long longint main(){
       int t,n;    scanf("%d",&t);    while(t--){
           scanf("%d",&n);        int i,j;        for(i=2;i<=n/2;i++){
               for(j=1;j
   

第三章 动态规划

背包问题

重点：不要看书上的代码！！！要看下面链接中的，书上的代码写的太差了。

01背包例题： n 为物品数，c 为背包承重，wi 为第 i 件物品的重量，vi 为第 i 件物品的价值。 𝑛=5, 𝑐=10, 𝑊={2,2,6,5,4}, 𝑉={6,3,5,4,6} 解答： 𝑝[6]={(0,0)} 𝑞[6]=𝑝[6]⊕(𝑤_5,𝑣_5)={(4,6)} 𝑝[5]={(0,0),(4,6)} 𝑞[5]=𝑝[5]⊕(𝑤_4,𝑣_4)={(5,4),(9,10)} 𝑝[4]={(0,0),(4,6),(9,10)} 𝑞[4]=𝑝[4]⊕(𝑤_3,𝑣_3)={(6,5),(10,11),(15,15)} 𝑝[3]={(0,0),(4,6),(9,10),(10,11)} 𝑞[3]=𝑝[3]⊕(2,3)={(2,3),(6,9)} 𝑝[2]={(0,0),(2,3),(4,6),(6,9),(9,10),(10,11)} 𝑞[2]=𝑝[2]⊕(2,6)={(2,6),(4,9),(6,12),(8,15)} 𝑝[1]={(0,0),(2,6),(4,9),(6,12),(8,15)} 选第1、2、5件物品，最大价值为15。

矩阵连乘

例题：找出从A1到A6的最少矩阵连乘的数量，及计算次序。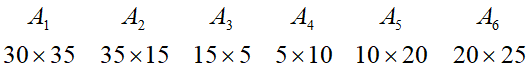 解答： 计算次序计算： 计算 m[1][1], m[2][2],…,m[6][6]; 计算 m[1][2], m[2][3],…,m[5][6]; 计算 m[1][3], m[2][4], m[3][5],m[4][6]; 计算 m[1][4], m[2][5],m[3][6]; 计算 m[1][5], m[2][6]; 计算 m[1][6]; 矩阵 m[i][j]表示 Ai 到 Aj 最小的连乘次数。 矩阵 s[i][j]表示 Ai 到 Aj 的最近一次分割点在 i 后。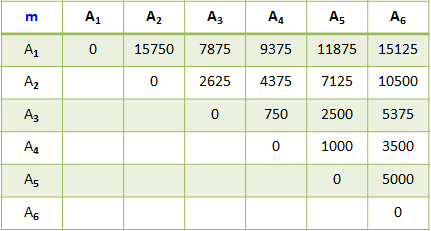 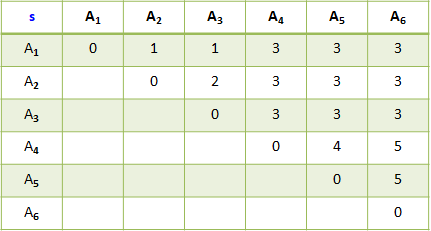通过 s 矩阵可知： A1 到 A3 在 A1 后分割，A1 到 A6 在 A3 后分割，A4 到 A6 在 A5 后分割， 即最优次序：(A1,(A2,A3,))((A4,A5,)A6)

最优三角剖分

给定一个凸多边形，以及定义在由多边形的边和弦组成的三角形上的权函数ω。求一个三角剖分，使得剖分中诸三角形上的权之和为最小。

跟矩阵连乘基本相似。 递推公式： 定义 t[i][j] 为凸子多边形剖分由 i 到 j 的最优解。

电路布线

递推公式：

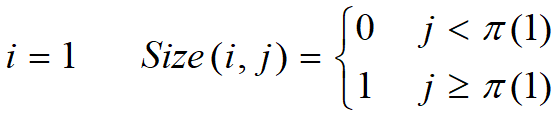
自顶向下计算最优值，在斜角值改变时可以取得所求的子集。即(9,10),(7,9),(5,5),(3,4)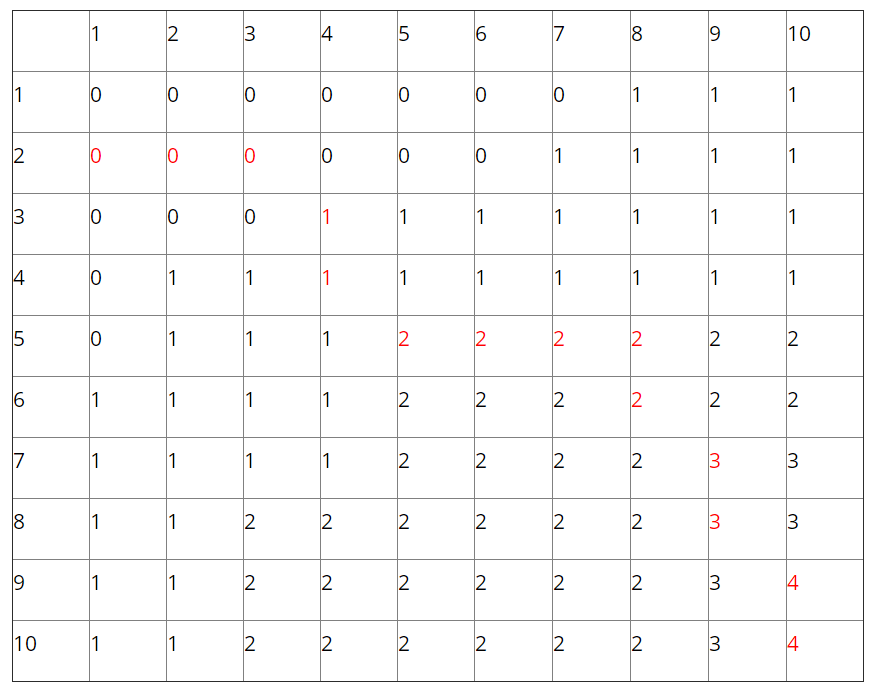

最长上升子序列

用的多了，一看就懂。

最大字段和

// a 为字段数组，这个代码，是不是一看就懂？	int sum=0, b=0;    for (int i=1; i<=n; i++) {
           if (b>0) b+=a[i];        else b=a[i];        if (b>sum) sum=b;    }

流水线作业

我更愿意称之为贪心水题。

我愿意分为三部分：

1. 第一个机器上的加工时间小于第二个机器上的加工时间，内部排序为在第一个机器上加工时间短的优先。
2. 第一个机器上的加工时间等于第二个机器上的加工时间在前排序，内部随便排。
3. 第一个机器上的加工时间大于第二个机器上的加工时间在前排序，内部随便排。

图论

习惯写图论了，可以直接用我之前写的blog，里面有代码、解释及实例。

最短路

1. 单源最短路
2. 多源最短路
   3.判负环的最短路

生成树

1. 稀疏图（点多边少）
2. 稠密图（点少边多）

附：dijkstra手写例题

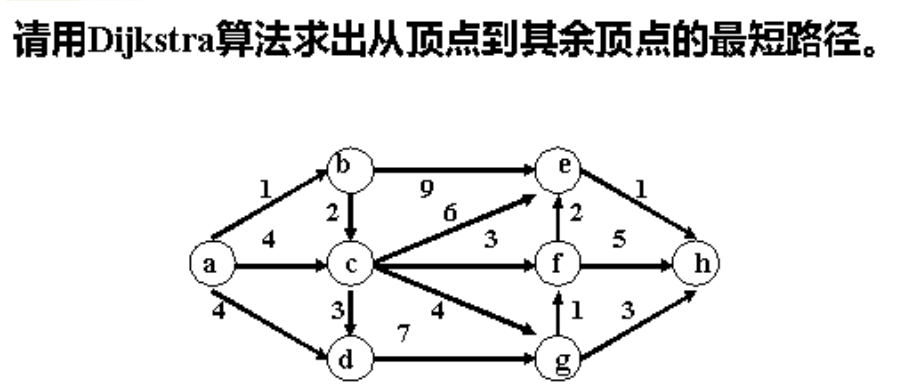
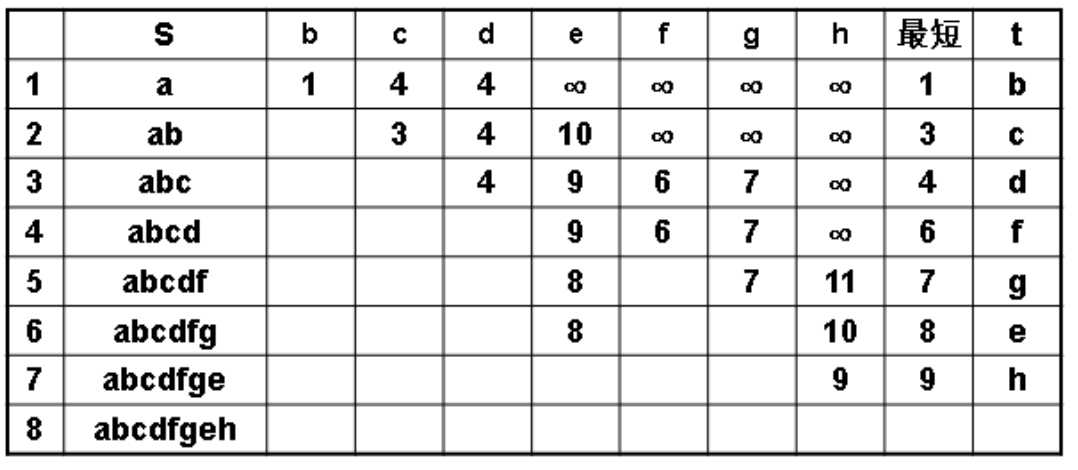
搜索

算法导论上应该只学 bfs，dfs 这种吧，说实话挺想听听舞蹈链是怎么讲的。

由于 bfs，dfs 我写的太多了，有很多不同情况的变种，只是两个方法而已，所以在此不写了，可以直接翻我发布的blog。

转载地址：https://blog.csdn.net/weixin_43820352/article/details/108650956 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！