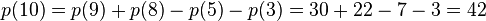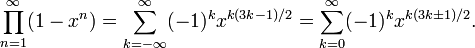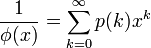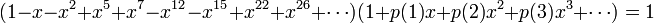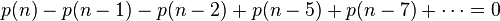五边形数定理是一个由发现的数学定理,描写叙述展开式的特性 。欧拉函数的展开式例如以下:
-
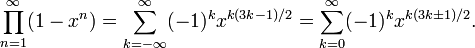
亦即
-

欧拉函数展开后,有些次方项被消去,仅仅留下次方项为1, 2, 5, 7, 12, ...的项次,留下来的次方恰为。
当中符号为- - + + - - + + .....
若将上式视为,其收敛半径为1,只是若仅仅是当作()来考虑,就不会考虑其收敛半径。
和切割函数的关系
欧拉函数的倒数是的,亦即:
-
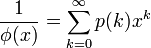
当中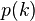 为k的切割函数。
为k的切割函数。
上式配合五边形数定理,能够得到
-
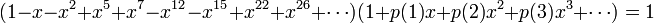
考虑 项的系数,在 n>0 时,等式右側的系数均为0,比較等式二側的系数,可得
项的系数,在 n>0 时,等式右側的系数均为0,比較等式二側的系数,可得
-
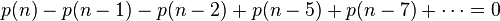
因此可得到切割函数p(n)的式
-

以n=10为例
-
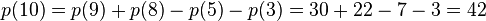
- 知道这个定理的话,hdu 4651就能够直接套模板了
-
#include #include #include #include #include #include #include #include #include
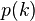 为k的切割函数。
为k的切割函数。 项的系数,在 n>0 时,等式右側的系数均为0,比較等式二側的系数,可得
项的系数,在 n>0 时,等式右側的系数均为0,比較等式二側的系数,可得